6장 3D Graphics - ① 3D에서 물체의 변환과 쿼터니언
6장에서는 2D 환경에서 완전한 3D 게임으로 전환하는 방법을 다룬다. 3D 게임으로 전환하기 위해서는 먼저 3D회전을 포함한 엑터의 변환을 다룰 수 있어야 한다. 또한 3D 모델을 로드하고 그릴 수 있어야 한다. 마지막으로 대부분의 3D 게임 장면에서 제공하는 여러 타입의 조명을 구현해야 한다.
💡 6장의 목차
- 3D에서 물체의 변환과 쿼터니언
- 3D 모델 로딩하기
- 3D 메시 그리기
- 조명
3D에서 물체의 변환
2D 환경을 3D환경으로 변경하기 위해서는 몇가지 변경해야 할 사항들이 있다. 그 중 첫번째가 좌표계 시스템을 바꿔야 한다. 2D 환경에서 우리는 \(x, y\) 평면 좌표계를 사용했다. 이 평면 좌표에서도 SDL을 사용할 때는 화면 상단이 \(-y\) 방향이었던 반면 OpenGL에서는 \(+y\) 방향으로 서로 상이 했다. 3D 좌표계 시스템은 당연히 \(x,y,z\) 3차원 좌표계를 사용한다. 그리고 이 3차원 좌표계에서도 각 좌표의 방향에 따라서 왼손 좌표계와 오른손 좌표계로 나뉜다. 우리는 이 두가지 좌표계 중에서 왼손좌표계를 사용할 예정이다.

3D 변환 행렬
3D 변환 행렬 중 스케일 변환 행렬과 이동 변환 행렬은 회전 변환 행렬에 비해 비교적 직관적으로 이해할 수 있다. 5장 변환과 행렬에서 다루었던 변환행렬에 다음과 같이 \(z\)요소만 추가하면 사용할 수 있다.
스케일 변환 행렬
스케일 변환행렬 \(S(s_x, s_y, s_z)\)는 다음과 같다.
\[S(s_x, s_y, s_z) =
\begin{pmatrix}
s_x & 0 & 0 & 0 \\
0 & s_y & 0 & 0 \\
0 & 0 & s_z & 0 \\
0 & 0 & 0 & 1\end{pmatrix}\]\[
\begin{pmatrix} x & y & z & 1\end{pmatrix}
\begin{pmatrix}
s_x & 0 & 0 & 0 \\
0 & s_y & 0 & 0 \\
0 & 0 & s_z & 0 \\
0 & 0 & 0 & 1\end{pmatrix} =
\begin{pmatrix} x \cdot s_x & y \cdot s_y & z \cdot s_z & 1\end{pmatrix}\]
이동 변환 행렬
이동 변환행렬 \(T(a,b,c)\)는 다음과 같다.
\[T(a, b, c) =
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
a & b & c & 1\end{pmatrix}\]\[
\begin{pmatrix} x & y & z & 1\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
a & b & c & 1\end{pmatrix} =
\begin{pmatrix} x + a & y + b & z + c & 1\end{pmatrix}\]
오일러 각과 쿼터니언
3D 상에서 회전을 표현하는 것은 2D 보다 복잡하다. 2D 평면상에서의 회전은 원점을 중심으로 (사실상 보이지 않는 \(z\)축을 중심으로)한 회전만 존재한다. 하지만 3D 공간상에서의 회전은 \(x\)축, \(y\)축, \(z\)축 각각에 대한 회전이 존재할 수 있다. 이렇게 총 3개의 축에 대한 회전 자유도를 가지는 것을 3자유도 회전이라고도 한다. 그리고 다음과 같이 각각의 회전축에 대한 회전을 표현하는 용어도 있다.
- 요(yaw): \(z\)축에 대한 회전
- 피치(pitch): \(y\)축에 대한 회전
- 롤(Roll) \(x\)축에 대한 회전
오일러 각의 회전 변환 행렬
오일러 각의 회전 변환 행렬에 대한 자세한 설명과 행렬 유도방법은 이 글을 참고하자. 각각 회전축에대한 회전 행렬 \(R_z(\theta), R_x(\theta), R_y(\theta)\)는 다음과 같다.
\[
\begin{pmatrix} x & y & z& 1\end{pmatrix}
R_z(\theta) =
\begin{pmatrix} x & y & z& 1\end{pmatrix}
\begin{pmatrix} \cos\theta & \sin \theta & 0 & 0 \\ -\sin \theta & \cos \theta & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}\]
\[
\begin{pmatrix} x & y & z& 1\end{pmatrix}
R_x(\theta)
= \begin{pmatrix}
x & y & z& 1\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos \theta & \sin \theta & 0 \\
0 & -\sin \theta& \cos\theta & 0 \\
0 & 0 & 0 & 1\end{pmatrix}\]
\[
\begin{pmatrix}
x & y & z& 1\end{pmatrix}R_y(\theta) = \begin{pmatrix}
x & y & z& 1\end{pmatrix}
\begin{pmatrix}
\cos\theta & 0 & - \sin \theta & 0 \\
0 & 1 & 0 & 0\\
\sin \theta & 0 & \cos\theta & 0 \\
0 & 0 & 0 & 1\end{pmatrix} \]
오브젝트의 실제 회전값은 각 축에 대한 별도의 회전 행렬을 만든 뒤 이 행렬들을 결합하여 구할 수 있다.
\[FinalRot = (RollMatrix)(PitchMatrix)(YawMatrix)\]
오일러 각의 문제
오일러 각을 3D 그래픽스에서 사용하게 될 경우 아래와 같은 문제점이 존재한다.
- 임의의 회전을 유도하는 것이 어렵다.
- 부드러운 보간이 어렵다.
- 짐벌락 현상이 발생한다.
임의의 회전을 유도하는 것이 어렵다
3차원 공간에서의 회전은 \(x,y,z\)축으로만 이루어지지 않는다. 임의의 회전 축으로도 회전 할 수 있어야 한다. 하지만 오일러 각만으로 임의의 회전을 계산하기는 쉬운일이 아니다.
부드러운 보간이 어렵다
\(P\)점에 있던 물체가 1초 동안에 \(P'\)으로 이동하는 움직임을 생각해보자. 물체가 순간이동 하지 않고 자연스럽게 이동하는 모습을 나타내기 위해서는 60프레임동안 각 프레임의 위치를 계산해야 한다. 즉 0 ~ 1초 사이의 임의의 시간 \(t\)에서의 물체의 위치를 계산 할 수 있어야 하고, 이 과정을 보간이라고 한다. 직선 운동에서의 보간을 선형 보간이라고 하고 원운동에서의 보간을 구면선형보간이라고 한다.
물체의 회전을 보간하기 위해서는 원운동에 해당하기 때문에 구면선형보간을 해야한다. 하지만 오일러 각을 사용할 경우 보간이 이상한 방향에서 나타나는 특이한 상황과 맞딱뜨릴 수 있다.
짐벌락 현상이 발생한다
이러한 3차원 구조물을 짐벌이라고 부른다.

3차원 회전에서 \(x,y,z\)축은 아래와 같이 각각 서로에게 종속적이다. 즉 한 축의 회전이 다른 축에 영향을 미칠 수 밖에 없다.

이때 특정 상황에서 두개의 축이 겹쳐 3자유도의 회전이 2자유도 회전이 되는 현상을 짐벌락 이라고 한다. 비록 특정한 경우에만 발생하지만, 과거에 나온 게임에서 짐벌락 현상이 발생하면 게임이 강제종료되는 문제까지도 발생했다. 때문에 당시 게임에서는 짐벌락현상을 피하기 위해서 오브젝트를 89도까지만 회전을 시키는 등의 방법을 사용하기도 했다.

다행이도 우리는 오일러 각의 문제를 해결할 수 있는 대안이 있고, 현재 대부분의 게임에서는 이 대안을 활용한다.
쿼터니언
오일러 각의 문제를 해결해줄 방법이 바로 쿼터니언(quaternion, 사원수) 이다. 쿼터니언을 수학적으로 설명하기란 쉽지 않다. 쿼터니언은 복소수를 사용하는 4차원 좌표계이기 때문에 직관적이지도 않고 계산도 상당히 복잡하다. 때문에 여기에서는 쿼터이언을 임의의 축에 대한 회전을 표현하는 방법 정도로 정의하고 수학적 설명보다는 게임에서 쿼터니언을 어떻게 활용 하는지 그 방법적인 측면에서 설명한다.
기본 정의
쿼터니언은 벡터\(q_v\)와 스칼라\(q_s\) 두 요소를 모두 가진다. 3D 그래픽에서의 쿼터이언은 스칼라 크기가 1인 특수한 쿼터니언을 사용한다. 쿼터니언\(q\)는 다음과 같이 표기한다.
\[q = [q_v, q_s] \]
앞에서 쿼터니언을 임의의 축에 대한 회전이라고 정의했다. 따라서 정규화 된 회전축 \(\hat a\)과 회전 각도 \(\theta\)로 쿼터니언을 이루는 벡터\(q_v\)와 스칼라\(q_s\)를 다음과 같이 계산할 수 있다.
\[q_v = \hat a \sin \frac{\theta}{2}\]
\[q_s = \cos \frac{\theta}{2}\]
쿼터니언을 활용한 회전
쿼터니언은 회전축으로 사용할 임의의 축 벡터와, 축에 대한 회전각의 크기(스칼라) 값으로 구성된다. 때문에 쿼터니언을 활용하기 위해서는 먼저 이 둘을 계산해야한다. 다음과 같은 상황을 가정해보자. 우주선이 위치\(s(-2,1,0)\)에서 \(\vec s <1,0,0>\)방향으로 이동중이다. 우주선이 운석을 향해서 \(p(-1,-1,3)\)로 회전시키려 한다. 이런 경우 오일러 각을 활용해서 계산할 수도 있지만, 쿼터니언을 활용하는 것이 훨씬더 안전하고 효과적이다.
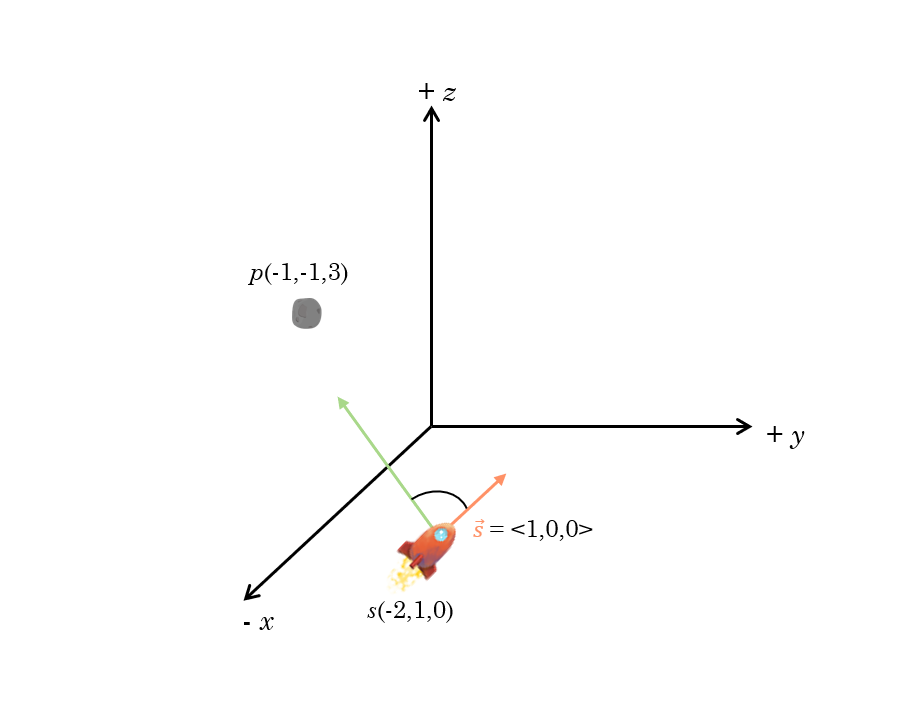
우리가 구해야 하는 값은 다음과 같다.
- 임의의 회전축 벡터 \(\hat a\)
- 회전축 \(\hat a\)기준의 회전각 \(\theta\)
이들을 구하기 위해서는 먼저 우주선이 향해야 하는 새로운 방향 \(NewFacing\) 벡터를 구해야 한다. 그리고 아래의 수식 처럼 이 \(NewFacing\) 벡터와 \(\vec s\)의 외적을 통해서 회전축 \(\hat a\)를 계산할 수 있고 내적을 통해서는 회전각\(\theta\)를 구할 수 있다.

이제 우주선이 운석을 향하는 회전을 나타내는 쿼터니언을 다음과 같이 생성할 수 있다. P가 어떤 위치에 있더라도 이 계산을 활용할 수 있다.
\[q = [q_v, q_s] = [\hat a \sin \frac{\theta}{2}, \cos \frac{\theta}{2}] \]
쿼터니언을 활용할 때 새롭게 향할 방향과 원래 향했던 방향이 평행한 경우가 있다. 이때는 외적의 결과로 0 벡터가 나오기 때문에 별도의 예외처리가 필요하다.
회전 결합
쿼터니언의 또 다른 일반 연산 중 하나는 기존 쿼터니언에 추가 회전을 적용하는 것이다. 두 쿼터니언 \(p, q\)으로 추가적인 회전을 구현하기 위해서는 그라스만 곱을 사용할 수 있다. 아래와 같이 곱할 경우 물체를 \(q\)로 회전한 뒤 \(p\) 로 회전시킨 결과와 같다. 그라스만 곱은 내부적으로 벡터의 외적을 사용하기 때문에 교환 법칙이 성립되지 않는다.
- 물체를 \(q\)로 회전한 뒤 \(p\)로 회전: \(pq\)
쿼터니언 회전의 결합을 위해서 저자가 제공해준 소스코드 Math.h에 있는 쿼터니언 곱셈함수 Concatenate를 사용할 수 있다.
Math.h
// q로 회전한 후 p로 회전
static Quaternion Concatenate(const Quaternion& q, const Quaternion& p);구면 선형 보간
구면 보간은 선형 보간과 다르게 보간된 값들은 항상 구면위에 존재해야 한다. 오일러 각은 이 구면보간이 쉽지 않지만, 사원수를 사용하면 보간이 매우 편리하다는 장점이 있다. 하지만 그 수학적 원리를 이해하기는 쉽지 않다. 그래서 수학적 계산은 생략하고 구면 보간 함수를 다음과 같이 사용할 수 있다는 점만 짚고 넘어간다. 두 쿼터니언 물체가 \(q_0\)에서 \(q_1\)으로 회전할때, 25% 정도 회전한 쿼터니언은 다음과 같이 구한다.
\[Slerp(q_0, q_1, 0.25)\]
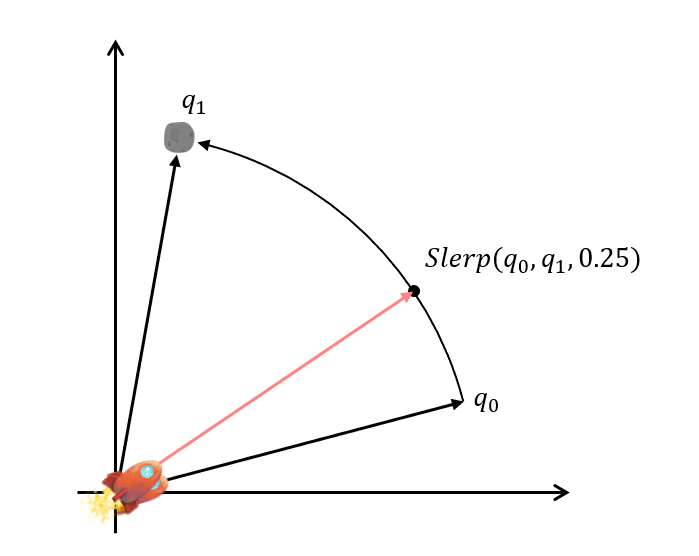
소스코드 상에서는 저자가 제공해준 소스코드 Math.h에서 다음과 같이 선언되어 있다.
Math.h
static Quaternion Slerp(const Quaternion& a, const Quaternion& b, float f);쿼터니언을 회전 행렬로
쿼터니언으로 회전을 계산하더라도 게임 세계는 변환 행렬을 사용하므로 쿼터니언을 코드에섯 사용하려면 다시 회전 행렬로 변환할 수도 있어야 한다. 이부분도 수학적 계산은 생략하고 소스 사용법만 짚고 넘어간다. 저자가 제공해준 소스코드 Math.h를 참고하면 쿼터니언 \(q\)에 대해서 회전 행렬로 변환하기 위한 함수를 다음과 같이 제공한다.
Math.h
static Matrix4 CreateFromQuaternion(const class Quaternion& q);출처:
에이콘 출판 <Game Programming in C++>
GS인터비전 출판 <게임 프로그래머를 위한 수학과 OpenGL 프로그래밍>
위키피디아

