5장 OpenGL - ③ 변환과 행렬변환(Transform)과 행렬(Matrix)
OpenGL은 25년 넘게 이어져온 2D/3D 크로스 플랫폼 그래픽을 위한 산업 표준 라이브러리이다. 이번 장에서는 OpenGL의 초기화, 삼각형의 사용, 셰이더 프로그램 작성, 변환을 위한 행렬 사용, 텍스처 지원 추가 등 컴퓨터 그래픽스의 여러 주제를 다룬다.
💡 5장의 목차
- OpenGL 초기화
- 삼각형 폴리곤
- 셰이더
- 변환과 행렬
- 텍스처 매핑
변환
10개의 운석을 그려야 하는 상황을 상상해보자. 앞서 배운것 것 처럼 10개의 버텍스 배열 개체를 정의하면 10개의 운석들을 그릴 수 있다. 10개의 서로 다른 버텍스 배열을 생성하고 버텍스 버퍼를 하나의 운석에 대응시킨 뒤 버텍스 버퍼의 필요에 따라 재계산하는 것이다. 하지만 이렇게 하면 메모리 사용 측면에서 낭비가 심하다. 버텍스 버퍼의 버텍스를 변경하고 변경된 내용을 OpenGL에 다시 알리는 것도 효율적이지 못하다. 우리는 더 효율적인 방법을 위해서 변환(transform)을 활용 할 수 있다.
모든 스프라이트는 궁극적으로 사각형에 텍스쳐를 입혀둔 것이다. 그래서 한번 생성한 이 사각형의 크기, 위치, 회전을 달리해서 그리게 되면 다양한 크기, 위치, 회전을 가진 운석을 여러개 생성해 내는것이 가능하다. 운석이 추가적으로 필요할 때마다 버텍스 배열을 새로 만들 필요도 없다. 이렇게 오브젝트의 크기, 위치, 회전값등을 바꾸는 것을 변환(Transform)이라고 한다.
오브젝트 공간
한 오브젝트를 만들때는 정규화된 장치 좌표로 버텍스 위치를 나타내지 않는다. 오브젝트 가 자체의 임의의 원점을 기준으로 오브젝트를 구성한다. 아래 그림에서 의자의 원점을 왼쪽 뒤쪽 다리 바닥으로 잡았다면 오른쪽 앞 다리는 (2,2,0), 등판읜 왼쪽 상단 모서리는 (0,0,4)에쯤에 위치한다고 할 수 있을 것이다. 책장이나 책상도 각자의 원점을 기준으로 좌표가 구성될 것이다. 이를 오브젝트 공간(object space) 혹은 모델 공간(model space)이라고 한다.

세계 공간
이 의자를 방이라는 레벨에 배치를 한다고 생각해보자. 방에도 임의의 원점이 있을 것이다. 이 원점에서 (5,5,0)에 이 의자를 배치한면 아래와 같이 배치될 것이다. 만약 같은 모델의 의자를 임의의점 (x,y,z)에 더 추가한다면 오브젝트 공간에서 만들어진 의자의 모든 버텍스 좌표에 동일하게 (x,y,z)값이 더해지는 이동 변환이 일어날 것이다. 만약에 의자가 넘어져있다면 회전변환이 일어날 수도 있을 것이다.

여기서 이방을 세계 공간이라고 하고 의자의 버텍스들은 오브젝트 공간에서 세계 공간으로 변환을 하였다. 이러한 좌표변환은 모든 버텍스에서 동일하게진행된다. 우리는 앞서 모든 버텍스에서 동일하게 실행되는 프로그램인 버텍스 셰이더를 배웠다. 버텍스 셰이더는 GPU에서 동작하는 프로그램이기에 병렬처리가 가능하여 속도도 빠르다. 앞으로 우리는 기본적인 변환의 개념을 다룬 후 버텍스 셰이더를 통해서 오브젝트 공간의 물체들을 세계공간에 배치하는 방법으 다룬다.
세계 공간으로 변환
오브젝트 공간에서 세계 공간으로 변환을 할때는 이동, 회전, 크기 변환이 일어난다. 변환을 수식으로 나타내기 위해서는 일반적으로 행렬을 이용한다. 행렬에서 벡터를 표현할때 선형대수학에서는 주로 열벡터를 사용한다. 하지만 여기서는 수식과 코드의 가독성을 위해서 행벡터를 사용한다. (행 벡터든 열벡터든 일관된 하나의 방식을 사용하면 문제될 것은 없다.)
스케일(Scale)
임의의 점 \((x,y)\)에 대해서 \(x\),\(y\) 값의 크기를 각각 조정할 수도 있다.

이러한 변환을 스케일 변환이라 하며 수식으로 나타내면 다음과 같다.
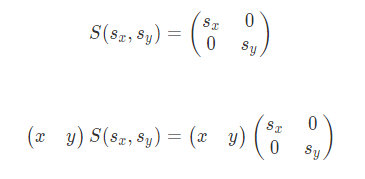
회전(Rotaion)
임의의 점 \((x,y)\)를 \(\theta\)만큼 회전하는 변환을 행렬로 나타내면 아래와 같다.

이동(Translation)
임의의 점 \((x,y)\) 이 주어졌을 때 이 점을 \((a,b)\) 만큼 이동시킨는 것은 조금 다르다. 스케일이나 회전처럼 \(2\times2\) 행렬이 아니라 아래처럼 \(1\times2\) 벡터의 덧셈 만으로 표현할 수 있기 때문이다.

동차 좌표계
만약 이동 변환도 곱셈으로 표현할 수 있다면 스케일 회전 이동 변환을 모두 곱해서 하나의 변환 행렬로 표현할 수 있다. 이동 행렬을 \(2\times2\)가 아닌 \(3\times3\)으로 표현하면 덧셈이 아닌 곱셈으로 표현할 수 있다.

이렇게 2차원 좌표 \((x,y)\)를 \((x,y,w)\) 로 표현한 것을 동차 좌표계라고 한다. 만약 3차원일 경우 \((x,y,z)\)를 \((x,y,z,w)\)로 표기하고 변환 행렬은 \(4\times4\) 행렬을 사용한다.
동차 좌표계를 사용하면서 얻는 가장 큰 장점은 모든 변환을 행렬의 곱으로 합성하여 하나의 변환행렬로 표현할 수 있다는 점이다. 우선 모든 변환 행렬을 곱하기 위해서는 스케일과 회전 변환도 \(3\times3\) 행렬로 만들어줄 필요가 있다.
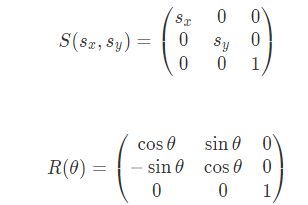
궁극적으로 우리가 원했던 도구는 오브젝트 공간에 있던 버텍스(정점)을 세계 공간으로 변환할 수 있는 일반식이었다. 그리고 우리는 이것을 행렬의 곱으로 표한할 준비를 마쳤다. 그 일반식을 나타내면 다음과 같다.
\[WorldTransform = S(s_x,s_y)R(\theta)T(a,b)\]
임의의 점 \((x,y)\)에는 다음과 같이 적용할 수 있다.
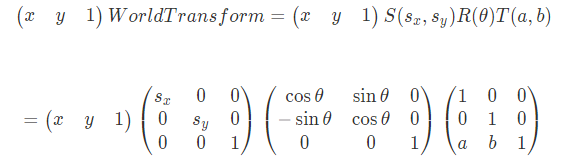
이때 유의할 점은 행렬에서 교환법칙은 성립하지 않는다는 점이다. 즉 회전 후 이동하는 것과 이동후 회전하는 것의 결과는 동일하지 않다. (회전을 할 때는 오브젝트 좌표를 중점으로 회전하는 것이 아니라 세계좌표계의 원점을 중심으로 회전한다.) 이를 그림으로 나타내면 다음과 같다. 회전변환을 이동 변환보다 늦게 적용하여서 물체의 위치가 우리가 원하던 위치에서 벗어났다.
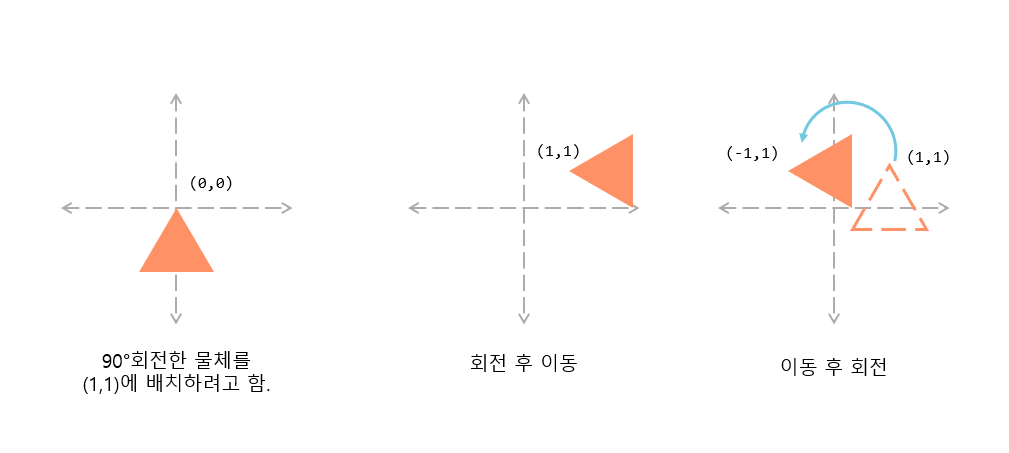
한 변환이 다른 변환에 간섭을 주지 않기 위해서는 반드시 위의 수식 처럼 스케일변환->회전 변환->이동 변환 순으로 진행(행렬의 곱)되어야 한다.
세계 공간에서 클립 공간으로 변환하기
버텍스 셰이더에서 앞서 우리가 구한 \(WorldTransform\) 행렬을 모든 버텍스에 곱해서 세계 공간으로의 변환을 진행할 것이다. 하지만 버텍스 셰이더의 역할은 하나 더 남았다. 버텍스 셰이더의 출력은 세계 공간에서 한 단계 더 변환이 진행된 클립공간(clip space) 이어야 한다(오브젝트 공간 → 세계 공간 → 클립 공간). 세계 공간을 클립공간으로 변환하기 위해서 뷰-투영 행렬을 사용하는데 이는 6장의 3D 그래픽스에서 더 다루고 지금 우리의 2D프로젝트에서는 간단한 뷰-투영 행렬만 사용해서 만들 수 있다.
우선 클립 공간은 정규화 되어있다는 특징이 있다. 그동안 우리의 2D 프로젝트에서는 \(1024\times768\) 크기의 세계공간 좌표를 사용하고 있었는데, 이 좌표계를 클립 공간 좌표로 변환하기 위해서는 왼쪽 하단부가 \((-1, -1)\) 우측 상단부가 \((1, 1)\)인 좌표계로 변환만 해주면 된다.

클립공간 변환 행렬인 \(SimpleViewProjection\)은 다음처럼 표현할 수 있다.
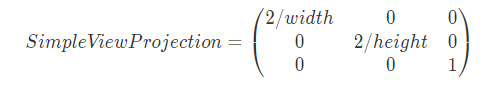
변환의 구현
최종적으로 버텍스 셰이더는 오브젝트 공간에서 세계 공간을 거쳐 클립공간으로 좌표계를 변환하기 위해서 아래의 연산을 진행해야 한다.
\[v' = v(WorldTransform)(SimpleViewProjection)\]
이를 코드로 나타내면 다음과 같다.
Transform.vert
#version 330
// uniform은 in, out 변수와 다르게 셰이더 프로그램의
// 수많은 호출 사이에서도 동일하게 유지되는 전역 변수이다.
// mat4 는 3차원 동차좌표계 변환 행렬인 4x4 행렬이다.
uniform mat4 uWorldTransform;
uniform mat4 uViewProj;
in vec3 inPosition;
void main()
{
vec4 pos = vec4(inPosition, 1.0);
gl_Position = pos * uWorldTransform * uViewProj;
}
C++로 glsl의 uniform 타입의 변수에 값을 입력하기 위해서는 다음 함수를 사용해야 한다.
glGetUniformLocation(셰이더 프로그램 ID, 변수명): 해당 셰이더 프로그램에서 변수를 찾아서GLuint타입의 uniform ID를 반환한다.glUniformMatrix4fv(uniform ID, 행렬의 수, 행벡터 여부, 행렬 데이터에 대한 포인터)해당 uniform에 행렬 데이터를 전달한다.
이 두 함수의 사용을 캡슐화한 SetMatrixUniform(const char*, const Matrix4&) 함수는 다음과 같다.
shader.cpp 의 Shader::SetMatrixUniform(const char*, const Matrix4&)
void Shader::SetMatrixUniform(const char* name, const Matrix4& matrix)
{
// 해당 이름의 uniform을 찾는다.
GLuint loc = glGetUniformLocation(mShaderProgram, name);
// 행렬 데이터를 uniform에 전송한다.
glUniformMatrix4fv(
loc, // uniform ID
1, // 행렬의 수 (이번 경우는 오직 하나)
GL_TRUE, // 행 벡터를 사용하면 TRUE로 설정
matrix.GetAsFloatPtr() // 행렬 데이터에 대한 포인터
);
}이제 Transform.vert 셰이더 프로그램의 uViewProj에 \(SimpleViewProjection\) 행렬 데이터를 입력해 보자. 먼저 \(SimpleViewProjection\)를 구해야한다. 저자는
\(SimpleViewProjection\) 행렬을 구할 수 있는 함수를 Math.h에 제공하고 있다.
Math.h의 Matrix4::CreateSimpleViewProj(float, float)
static Matrix4 CreateSimpleViewProj(float width, float height)
{
float temp[4][4] =
{
{ 2.0f / width, 0.0f, 0.0f, 0.0f },
{ 0.0f, 2.0f / height, 0.0f, 0.0f },
{ 0.0f, 0.0f, 1.0f, 0.0f },
{ 0.0f, 0.0f, 1.0f, 1.0f }
};
return Matrix4(temp);
}\(SimpleViewProjection\)은 게임이 실행되고 셰이더가 로딩될때 한번만 계산하면 된다. 때문에 Game::LoadShader()함수에서 다음과 같이 셰이더 로딩과 함께 계산하고 Transform.vert 셰이더 프로그램의 uViewProj에 값을 전달해 주자.
Game.cpp의 Game::LoadShader()
bool Game::LoadShader()
{
mSpriteShader = new Shader();
if (!mSpriteShader->Load("Shaders/Transform.vert", "Shaders/basic.frag"))
{
return false;
}
mSpriteShader->SetActive();
// 화면 너비가 1024x768인 view proj 변환행렬
Matrix4 viewProj = Matrix4::CreateSimpleViewProj(1024.f, 768.f);
mSpriteShader->SetMatrixUniform("uViewProj", viewProj);
return true;
}이제 앞서 다뤘던 오브젝트 공간-> 세계 공간으로의 변환을 다뤄보자. 앞서 세계 공간 변환 행렬을 다음과 같이 나타냈었다.
\[WorldTransform = S(s_x,s_y)R(\theta)T(a,b)\]
이를 코드로 나타내면 다음과 같다.
Actor.cpp의 void Actor::ComputeWorldTransform()
void Actor::ComputeWorldTransform()
{
if (mRecomputeWorldTransform)
{
mRecomputeWorldTransform = false;
// 스케일, 회전, 이동 행렬 순으로 결합해서 세계 변환 행렬 구함
mWorldTransform = Matrix4::CreateScale(mScale);
mWorldTransform *= Matrix4::CreateRotationZ(mRotation);
mWorldTransform *= Matrix4::CreateTranslation(Vector3(mPosition.x, mPosition.y, 0.0f));
}
}이렇게 계산된 세계변환 \(4\times4\) 행렬 mWorldTransform은 아래와 같이 버텍스 셰이더에 전달되어서 모든 버텍스에 대해서 엑터의 위치, 회전, 크기를 계산하게 된다.
SpriteComponent.cpp의 SpriteComponent::Draw(Shader*)
void SpriteComponent::Draw(Shader* shader)
{
// 텍스처의 너비와 높이로 사각형을 스케일
Matrix4 scaleMat = Matrix4::CreateScale(
static_cast<float>(mTexWidth),
static_cast<float>(mTexHeight),
1.0f);
Matrix4 world = scaleMat * mOwner->GetWorldTransform();
// 세계 변환 행렬을 설정
shader->SetMatrixUniform("uWorldTransform", world);
// 사각형을 그린다.
// glDrawElements 호출을 위해서는 활성화된 버텍스 배열 개체와 활성화된 셰이더가 필요하다.
// 매 프레임에서 SpriteComponents를 그리기 전에 스프라이트 버텍스 배열개체와 셰이더 모두를 활성화 해야한다.
glDrawElements(
GL_TRIANGLES, // 그려야 할 폴리곤 타입
6, // 인덱스 버퍼에 있는 인덱스의 수
GL_UNSIGNED_INT,// 각 인덱스의 타입
nullptr // nullptr
);
}
여기까지 진행하면 교재에 나와있는것 처럼 다음과 같은 화면을 얻을 수 있다.
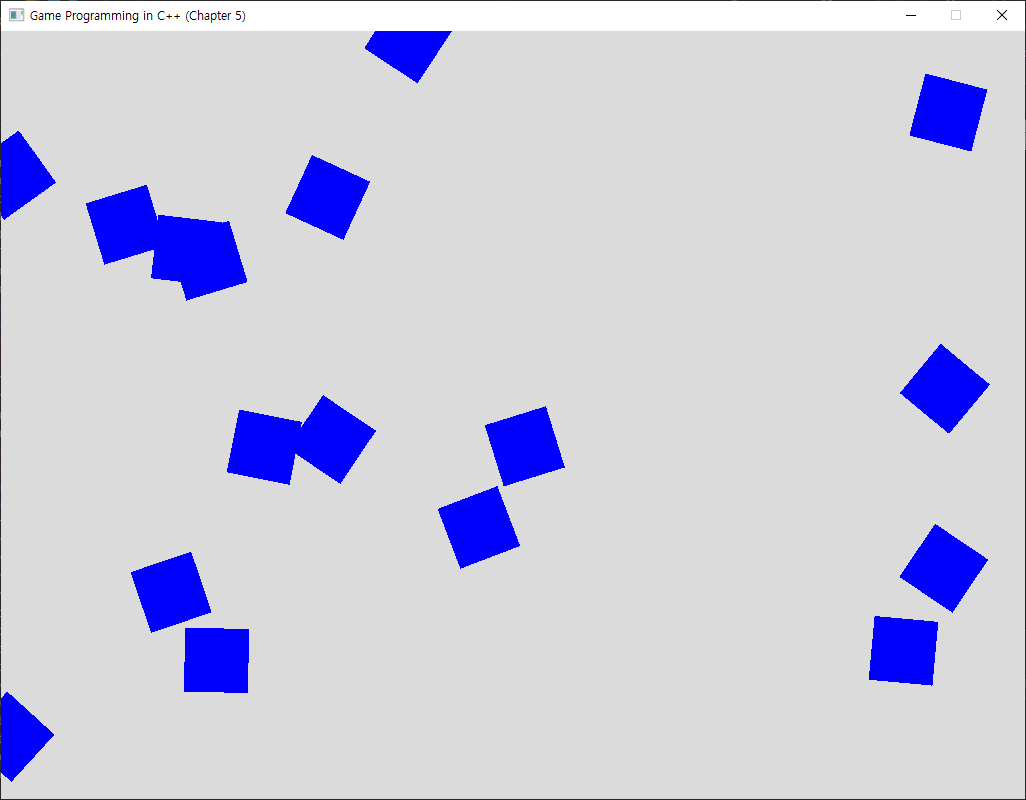
여기에 설명된 부분외에도 일부 변경된 코드들이 있다. 이는 전체 소스코드를 참고 하자.
현재는 전부 파랑색 사각형으로 보이지만 이들은 아직 텍스쳐를 입히기 전인 우주선과 운석의 sprite 들이다. 3장에서 사용했던 조작방식 그대로 잘 움직이고 레이져도 발사하는 것을 확인할 수 있을 것이다. 변환에 대한 설명은 여기서 마치고 다음 글에서는 텍스처에 대해서 다루도록 한다.
본 게시글은 에이콘 출판사의 Game Programming in C++ 도서를 학습하며 요약 정리한 내용입니다.
