3차원 회전 변환 행렬 (유도하는 방법)
게임 프로그래밍을 포함한 3D 그래픽스에서 변환은 매우 중요한 개념이다. 최근에는 상용엔진이 많이 보급되어서 직접 변환값을 계산하지 않고 엔진에서 제공해주는 간단한 함수들 만으로도 원하는 위치에 원하는 회전상태와 크기로 물체를 출력할 수 있게됐다. 하지만 이 엔진들이 제공해주는 간단한 함수들의 내부에는 모두 변환이라는 개념을 포함하고 있기 때문에 엔진을 단순히 사용하는 것을 넘어서 그 원리를 이해하거나 혹은 상용엔진으로 부터 독립적인 3D그래픽을 만들고자 한다면 반드시 짚고 넘어가야할 내용이다.
대부분 수학에서는 벡터를 다룰때 열벡터를 사용하지만, 여기에서는 행벡터를 사용하고자 한다. 열벡터를 사용할 경우 수학으로 표기할때 가독성이 좋고, 행벡터로 표기할 경우 변환행렬들을 추상화 한 후 합성행렬을 구하는 과정에서 가독성이 높다. 원칙적으로는 열벡터를 사용하던지 행벡터를 사용하던지 하나의 방법을 일관적으로 사용한다면 문제되지 않는다.
이번 글에서는 변환 중에서도 상대적으로 복잡한 회전변환에 대한 설명과 공식 유도를 다뤄볼 예정이다. 회전 변환을 다루기에 앞서서 먼저 스케일 변환과 이동 변환을 정리하면 다음과 같다.
스케일 변환
2차원에서의 스케일 변환\(S(s_x, s_y)\)를 동차좌표계 행렬로 표현하면 다음과 같이 나타낼 수 있다. (3차원은 \(s_z\)를 추가해서 \(4\times 4\)행렬로 표현 하면 된다.)
\[S(s_x, s_y) = \begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1 \end{pmatrix}\]
\[\begin{pmatrix} x & y & 1\end{pmatrix}\begin{pmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & 1\end{pmatrix} = \begin{pmatrix} s_x\cdot x & s_y\cdot y & 1 \end{pmatrix}\]
이동 변환
2차원에서 이동 변환\(T(t_x,t_y)\)를 동차 좌표계 행렬로 표현하면 다음과 같이 나타낼 수 있다. (3차원은 \(t_z\)를 추가해서 \(4\times 4\) 행렬로 표현 하면 된다.)
\[T(a,b) = \begin{pmatrix} 1 & 0 & 0 \\0 & 1 & 0 \\ t_x & t_y & 1 \end{pmatrix}\]
\[\begin{pmatrix} x & y & 1\end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\0 & 1 & 0 \\ t_x & t_y & 1 \end{pmatrix} = \begin{pmatrix} x + t_x & y + t_y & 1\end{pmatrix}\]
스케일 변환과 이동 변환, 동차좌표계에 대한 추가적인 설명이 필요하다면 이 글을 참고하자.
회전 변환
회전 변환은 이동변환이나 스케일 변환처럼 직관적이지 않아서 조금 구체적으로 다뤄볼 예정이다.
2차원에서 회전 변환
우선 2차원에서의 회전 변환을 먼저 살펴보자. 원래의 좌표가 \((x, y)\)인 점 \(P\)가 있을때, 이 점을 \(\theta\)만큼 회전한 점 \(P'\)의 좌표는 \((x',y')\) 라고 하자. 원점에서 원래의 좌표 \((x,y)\)에 선분을 그으면, 이 선분은 어떤 길이 \(r\)을 가지고 \(x\)축과 이루는 어떤 각도 \(\phi\)를 가질 것이다.
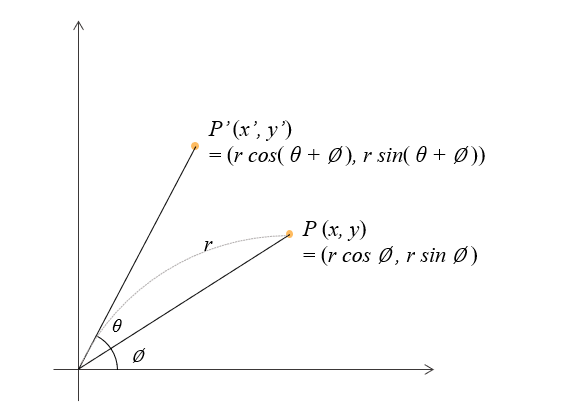
이때 점 \(P\)의 \(x\)좌표와 \(y\)좌표를 \(r\)과 \(\phi\)로 표현하면 다음과 같을 것이다.
\[x = r \cos \phi \] \[y = r \sin \phi \]
점 \(P\)를 \(\theta\)만큼 회전한 점 \(P'\)의 \(x'\)좌표와 \(y'\)좌표를 \(r\)과 \(\phi\), \(\theta\)로 표현하면 다음과 같다.
\[x' = r \cos (\phi+\theta) \] \[y' = r \sin (\phi+\theta) \]
이를 삼각함수의 덧셈 정리를 활용해서 풀어 쓸 수 있다. 참고로 삼각함수의 덧셈 정리는 다음과 같다.
\[\cos(a+b) = \cos a \cos b - \sin a \ sin b\] \[\sin(a+b) = \sin a \cos b + \cos a \sin b\]
이를 \(x', y'\)에 적용해 보자.
\[x' = (r \cos\phi) \cos \theta - (r \sin \phi) \sin \theta = x \cos \theta - y \sin \theta\] \[y' = (r \cos\phi) \sin \theta + (r \sin \phi) \cos \theta = x \sin \theta + y \cos \theta \]
이렇게 표현할 수 있다. 이를 동차행렬 식으로 정리 해보자.
\[\begin{pmatrix} x & y & 1\end{pmatrix}\begin{pmatrix} \cos\theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1\end{pmatrix} = \begin{pmatrix} x\cos \theta - y\sin \theta & x \sin \theta + y \cos \theta & 1 \end{pmatrix}\]
이렇게 2차원에서 회전에 대한 변환행렬을 \(\theta\)에 대해서 정리할 수 있다.
\[R(\theta) = \begin{pmatrix} \cos\theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1\end{pmatrix}\]
3차원에서 회전변환
2차원에서 회전 변환의 중심 원점이었다. 3차원에서의 회전 변환에서 회전 중심축은 \(x\)축, \(y\)축, \(z\)축 처럼 하나의 직선이다. 위에서 보인 2차원에서의 회전을 3차원 공간에서의 회전변환으로 확장해서 생각해볼 수도 있다. 사실 위에서 보인 회전은 아래와 같이 3차원 공간에서 \(z\)축을 중심으로 한 \(xy\) 평면에서의 회전과 동일하다. 그리고 \(z\)을 중심으로 회전을 진행했을 때 \(z\)축의 좌표는 변하지 않는다는 것도 살펴 볼 수 있다.
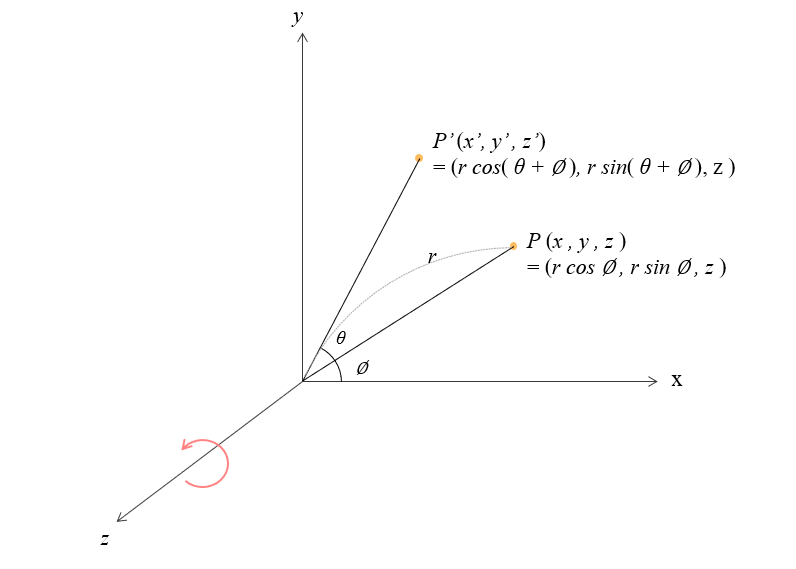
따라서 z축을 중심으로 회전변환을 2차원 \(xz\)평면상 회전변환에 \(z\)축 성분을 유지형태로 다음과 같이 이루어 진다는 것을 알 수 있다. 이를 수식으로 표현하면 다음과 같다.
\[x' = \cos \theta \cdot x - \sin \theta \cdot y+ 0 \cdot z \] \[y' = \sin \theta \cdot x + \cos \theta \cdot y + 0 \cdot z \] \[z' = \qquad 0 \cdot x \quad + 0 \cdot y + 1 \cdot z\]
이를 행렬로 표현하면 다음과 같다.
\[\begin{pmatrix} x' & y' & z' & 1 \end{pmatrix} = \begin{pmatrix} x & y & z& 1\end{pmatrix}\begin{pmatrix} \cos\theta & \sin \theta & 0 & 0 \\ -\sin \theta & \cos \theta & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix} \]
즉 \(R_z(\theta)\)는 다음과 같이 표현할 수 있다.
\[R_z(\theta) = \begin{pmatrix} \cos\theta & \sin \theta & 0 & 0 \\ -\sin \theta & \cos \theta & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}\]
다음으로는 \(x\)축과 \(y\)축을 기준으로 회전변환 식을 유도해보겠다. \(y\)축을 기준으로 회전 변환을 한다는 것인 결국 \(z\)축을 기준으 회전변환을 하는 식에 \(y\)은 \(x\)값으로 \(x\)값은 \(z\)값으로 \(z\)값은 \(y\)값으로 전환하는 것과 동일하다.

이 그림을 식으로 나타내면 다음과 같다.
\[z' = \cos \theta \cdot z - \sin \theta \cdot x+ 0 \cdot y \] \[x' = \sin \theta \cdot z + \cos \theta \cdot x + 0 \cdot y \] \[y' = \qquad 0 \cdot z \quad + 0 \cdot x + 1 \cdot y\]
위 식을 알파뱃 순서로 재배열하면 다음과 같다.
\[x' = \cos \theta \cdot x + 0 \cdot y + \sin \theta \cdot z\] \[y' =\qquad 0 \cdot x + 1 \cdot y \quad + 0 \cdot z \] \[z' = - \sin \theta \cdot x+ 0 \cdot y + \cos \theta \cdot z \]
이를 행렬로 표현하면 다음과 같다.
\[\begin{pmatrix} x' & y' & z' & 1 \end{pmatrix}
= \begin{pmatrix}
x & y & z& 1\end{pmatrix}
\begin{pmatrix}
\cos\theta & 0 & - \sin \theta & 0 \\
0 & 1 & 0 & 0\\
\sin \theta & 0 & \cos\theta & 0 \\
0 & 0 & 0 & 1\end{pmatrix} \]
즉, \(y\)축을 기준으로한 회전변환 \(R_y(\theta)\)행렬은 다음과 같이 나타낼 수 있다.
\[ \begin{pmatrix} x & y & z& 1\end{pmatrix}R_y(\theta) = \begin{pmatrix}
x & y & z& 1\end{pmatrix}
\begin{pmatrix}
\cos\theta & 0 & - \sin \theta & 0 \\
0 & 1 & 0 & 0\\
\sin \theta & 0 & \cos\theta & 0 \\
0 & 0 & 0 & 1\end{pmatrix} \]
같은 방식으로 \(x\)축을 기준으로 회전변환에 대해 계산하면 \(R_x(\theta)\)를 다음과 같이 구할 수 있을 것이다.
\[\begin{pmatrix} x & y & z& 1\end{pmatrix}R_x(\theta)
= \begin{pmatrix}
x & y & z& 1\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos \theta & \sin \theta & 0\\
0 & -\sin \theta & \cos\theta & 0 \\
0 & 0 & 0 & 1\end{pmatrix}\]
출처:
에이콘 출판 <Game Programming in C++>
