[BOJ 1002] (기하) 터렛 (C++)

터렛 (Silver 4)

문제

전체 문제 보기

1002번: 터렛

접근법

이 문제에서 마린이 존재할 수 있는 위치라는 것은 결국 터렛의 각 좌표를 원의 원점, 마린까지 거리를 원의 반지름으로 하는 두 개의 원의 교점 개수를 묻는 것과 동일하다. 원의 교점은 아래와 같이 7가지의 경우가 존재할 수 있다.

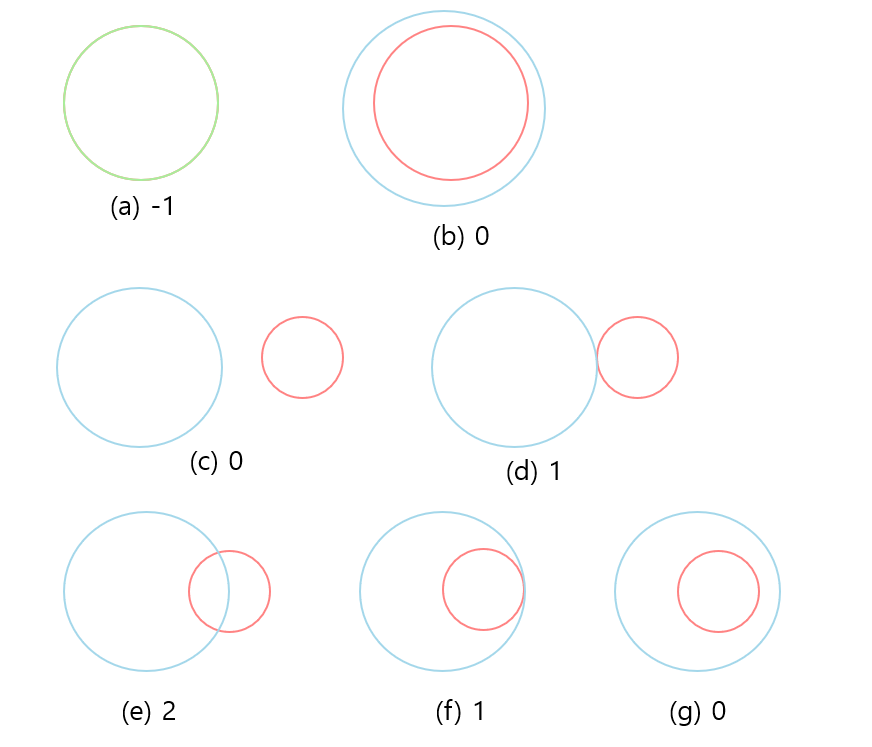
• (a)와 (b)는 두 원의 원점이 같은 경우이다. 이때 반지름 길이도 같다면 두 원이 겹쳐서 교점의 수가 무한이 되고, 반지름이 다르다면 교점이 없다.
• (c)는 두 원의 중심의 거리가 두 원의 반지름 합보다 큰 경우이다. 교점이 발생할 수 없다.
• (d)는 두 원의 중심의 거리가 두 원의 반지름 합과 같은 경우이다. 교점이 1개 발생한다.
• (e)는 두 원의 중심의 거리가 두 원의 반지름 차 보다 큰 경우이다. 교점이 2개 발생한다.
• (f)는 두 원의 중심의 거리가 두 원의 반지름 차와 같은 경우이다. 교점이 1개 발생한다.
• (g)는 두 원의 중심의 거리가 두 원의 반지름 차 보다 작은 경우이다. 교점이 발생하지 않는다.

이를 코드로 구현하면 다음과 같다.

구현

계산비용이 큰 제곱근 함수 사용을 피하기 위해서 각각 거리의 제곱으로 비교하였다.

#include <iostream>
#include <cmath>
using namespace std;

struct Circle {
    Circle() : x(0), y(0), r(0) {}
    int x, y, r;
};

int main() {
    // 입출력 성능향상을 위한 설정 
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);

    int T;

    Circle a, b;

    cin >> T;

    while (T--)
    {
        int answer = 0;

        cin >> a.x >> a.y >> a.r;
        cin >> b.x >> b.y >> b.r;

        int sqrDistance = (a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y);
        int sqrSumOfRadius = (a.r + b.r) * (a.r + b.r);

        if (sqrDistance == 0)  // 두 원의 중심이 같은 경우
        {
            if (a.r == b.r) // 반지름이 같으면 무한
                answer = -1;
            else            // 반지름이 다르면 교점 x
                answer = 0;
        }

        // 중심의 거리가 반지름의 합보다 크다면 안만남  
        else if (sqrDistance > sqrSumOfRadius)
            answer = 0;

        // 중심간의 거리와 반지름의 합이 같다면 한 점에서만 만남.
        else if (sqrDistance == sqrSumOfRadius)
            answer = 1;

        // 중심간의 거리가 반지름의 합보다 작다면 여러 경우가 있음.
        else if(sqrDistance < sqrSumOfRadius)
        {
            // 중심간의 거리가 두 반지름의 차 보다 크다면
            if (sqrDistance > (a.r - b.r) * (a.r - b.r))
                answer = 2;

            // 중심간의 거리가 두 반지름의 차와 같다면
            else if (sqrDistance == (a.r - b.r) * (a.r - b.r))
                answer = 1;

            // 중심간의 거리가 두 반지름의 차보다 작다면
            else if(sqrDistance < (a.r - b.r) * (a.r - b.r))
                answer = 0;
        }

        cout << answer << endl;       
    }
    return 0;
}