[BOJ 2156] (동적계획법) 포도주 시식 (C++)

포도주 시식(Silver 1)

문제

전체 문제 보기

2156번: 포도주 시식

접근법

이 문제에서 구해야 하는 값은 주어진 규칙에 따라 포도주를 시식할 때 마실 수 있는 포도주의 최댓값이다. 주어진 규칙은 다음과 같다.

• 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
• 연속으로 놓여 있는 3잔을 모두 마실 수는 없다.

이를 일반화 해서 생각해 보자. n개의 포도주잔이 있을 때 n번째 잔을 마시는 것이 좋을지 마시지 않는 것이 좋을지 우리는 판단할 수 있어야 한다.

포도주를 연속해서 3잔을 마실 수 없기 때문에 n번째 포도주를 마실지 말지 판단하기 위해서는 3가지 경우를 따져야 할 것이다.

• n-1번 포도주 까지 마시고, n 번 포도주를 마시지 않는다.
• n-2번 포도주 까지 마시고, n-1번 포도주를 마시지 않고, n 번 포도주를 마신다.
• n-3번 포도주 까지 마시고, n-2번 포도주를 마시지 않고, n-1번, n번 포도주를 마신다.

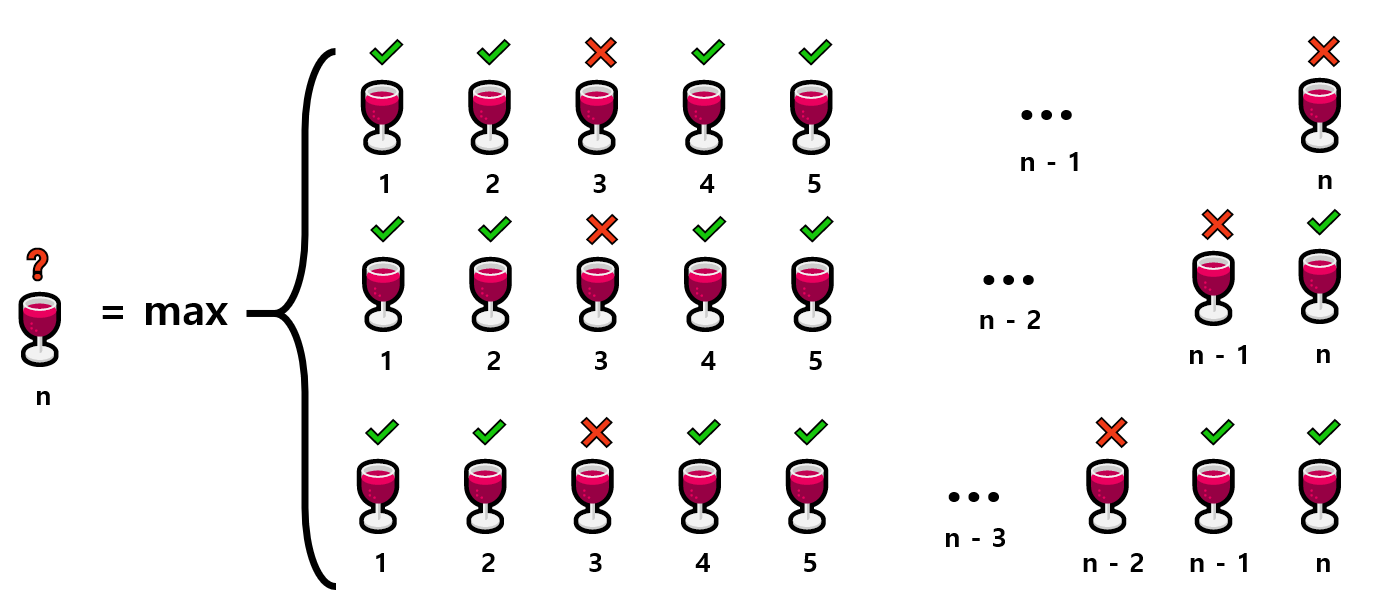
이를 점화식으로 표현하면 다음과 같다.

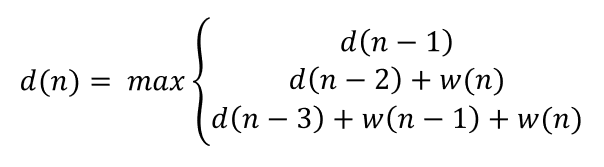
여기서 직관적으로 잘 이해되지 않는 부분이 있을 수 있다. "n-1번 포도주 까지 마시고 n 번 포도주를 마시지 않는다."에서 만약 n-1번 포도주까지의 최댓값이 n-1번 포도주를 마시지 않는 결정이었다면 "n-1번 포도주 까지의 최대로 마시고 n번 포도주도 마신다."의 경우의 수가 포함되지 않는 것 아니냐?라고 생각할 수도 있다. 이는 한번 더 생각해야 하기 때문에 직관적으로 이해하기는 어렵다. 이 부분에 대해서는 이렇게 생각해보자. n-1번 포도주까지의 최댓값이 n-1번 포도주를 마시지 않는 결정일 수는 있으나, 그렇다면 결국 n-1번 포도주까지의 최댓값 중, n-1번 포도주를 마시지 않는 결정은 n-2번 포도주까지의 최댓값과 같은 값이다. 그리고 우리는 n-2번 포도주 까지 마시고 n번 포도주를 마시는 경우를 두 번째에 반영하였기 때문에 "n-1번 포도주 까지의 최대로 마시고 n번 포도주도 마신다."도 고려되어 있다.

 

점화식을 살펴보면 d(n)을 구하기 위해서 d(n-1), d(n-2), d(n-3)의 값을 계산해야 한다. d(n-1), d(n-2), d(n-3) 값들도 각각 d(n-2), d(n-3), d(n-4)... 등의 계산을 요구한다. 만약 그때마다 해당 값들을 새로 계산해야 한다면 계산량은 \(O(3^n)\)이 될 것이고 이는 사용할 수 없을 정도로 많은 계산량을 요구한다. 때문에 동적계획법을 활용하여 한 번 계산한 d(n)값은 다시 계산하지 않도록 배열에 저장하자. 그러면 계산량은 \(O(n)\)으로 많이 개선될 수 있다.

구현

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);
    unsigned int n;
    cin >> n;
    vector<int> w(n+1);  // n개의 포도주 (1 ~ n개 사용)
    vector<int> d(n+1);  // 계산결과 저장할 배열 (1 ~ n개 사용)

    for (size_t i = 1; i < n+1; ++i)
    {
        cin >> w[i];
    }

    // 초기값 설정
    d[0] = 0;
    d[1] = w[1];
    d[2] = w[1] + w[2];

    for (size_t i = 3; i < n+1; i++)
    {
        const int a = d[i - 1];
        const int b = d[i - 2] + w[i];
        const int c = d[i - 3] + w[i - 1] + w[i];

        d[i] = max({ a, b, c });
    }

    cout << d[n];

    return 0;
}