본문으로 바로가기

[BOJ 5670] (Trie) 휴대폰 자판(C++)

category Algorithms/Trie 2021. 8. 7. 16:28

휴대폰 자판(Platinum 4)

문제

전체 문제 보기

 

5670번: 휴대폰 자판

휴대폰에서 길이가 P인 영단어를 입력하려면 버튼을 P번 눌러야 한다. 그러나 시스템프로그래밍 연구실에 근무하는 승혁연구원은 사전을 사용해 이 입력을 더 빨리 할 수 있는 자판 모듈을 개발

www.acmicpc.net

접근법

이 문제는 정렬을 활용해서 풀 수도 있고, 트라이를 활용해서도 풀 수 있다. 트라이 문제들 중에서는 이렇게 정렬 풀 수 있는 경우가 많은 것 같다. 필자는 이번 문제를 트라이로 풀었다. 트라이는 문자열의 접두어를 활용하는 문제 해결에 특화된 자료구조이다. 이번 문제에서도 자동 입력이라고 표현된 기능은 결국 중복된 접두어를 입력해주는 기능이기 때문에 트라이를 풀이했을 때 효율이 좋다고 판단했다.

자료구조 선택

이 문제에 맞춰서 트라이의 기본적인 삽입 탐색 함수를 조금 수정하여 풀수 있다. (기본적인 트라이 구조는 이 글을 참고하자.)우선 Node 구조체에서 자식 노드들을 배열을 사용하여 다음과 같이 정의한다. 자식 노드를 unordered_map으로도 사용해 봤는데 1초 시간제한에서 924ms라는 결과가 나왔다. 시간이 너무 빠듯해 보여서 최대한 속도를 높일 수 있는 배열을 활용한 인덱싱 방식이 더 적합하다고 판단하였다. 트라이 탐색에서 자식 노드 개수가 필요하기 때문에 numChild 변수를 추가하였다.

struct Node {
    Node() : isEnd(false), links{}, numChild(0)
    {}

    array<Node*, 26> links;
    bool isEnd;
    int numChild;
    static size_t GetIndex(char ch) { return ch - 'a'; }
};

다음으로 Trie 클래스에서 다음과 같이 선언한다. 생성자에서는 root 노드를 생성하고, 문자열을 입력받는 Insert함수와 문제 풀이 함수 Solution 함수를 선언한다. Solution함수 내부적으로는 전위탐색을 재귀적으로 호출하여 문제를 풀 예정이다. 또한 Node를 동적으로 활용하기 때문에 소멸자에서 동적 생성된 Node를 반드시 해제해야한다. 여러 테스트 케이스에 대해서 테스트가 진행되는데 동적 생성된 노드를 해제하지 않는다면 어마 어마한 메모리 누수가 발생할 수 있다. 그리고 이번 문제 풀이를 위해서 트라이의 전체 노드 개수를 저장하는 변수 size와 자동 완성을 위해 입력해야하는 총 input 수를 저장하는 totalInput을 선언한다.

class Trie {
public:
    Trie() : totalInput(0), size(0) { root = new Node(); }
    ~Trie() { DeleteLinks(root); }
    void Insert(const string& word);
    float Solution();

private:
    void PreorderTraverse(Node* node, int inputCnt);  // 노드 탐색을 위한 재귀함수
    void DeleteLinks(Node* node);   // 전체 노드 삭제를 위한 제귀함수
    Node* root;
    int totalInput; // 자동완성을 위해서 입력해야하는 총 input 수 
    int size;   // 문자열의 개수
};

Trie 클래스는 main 함수에서 다음과 같이 활용된다.

int main()
{
    // 입출력 성능 향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);
    // 소수 둘째자리 까지 출력을 위한 설정
    cout.precision(2);
    cout << fixed;

    size_t N;  // 입력 받을 문자열 개수
    while (cin >> N)
    {
        Trie trie;

        for (size_t i = 0; i < N; ++i)
        {
            string word;
            cin >> word;
            trie.Insert(word);
        }
        cout << trie.Solution() << endl;
    }
    return 0;
}

구현

Insert 함수

Insert 함수는 기본적인 트라이의 삽입 함수와 비슷하다. 여기서는 Iterative 한 방식으로 구현하였다. 정답 출력 시 평균을 출력해야 하기 때문에 평균값을 계산하기 위한 전체 문자열 개수 size를 문자열 하나 입력할 때마다 1씩 증가시켜준다는 특징이 있다. 그리고 자식 노드를 하나 생성할 때마다 numChild 값을 1 증감시켜준다.

void Trie::Insert(const string& word)
{
    Node* cur = root;
    for (size_t i = 0; i < word.length(); ++i)
    {
        size_t idx = Node::GetIndex(word[i]);
        if (cur->links[idx] == nullptr)
        {
            cur->links[idx] = new Node();
            cur->numChild++;
        }
        cur = cur->links[idx];
    }
    cur->isEnd = true;
    size++;
}

PreorderTraverse 함수 구현

PreorderTraverse 함수는 매개변수로 최종 정답을 출력할 Solution 함수에서 아래와 같이 사용될 함수이다.

float Trie::Solution()
{
    totalInput = 0;

    // root 노드의 모든 자식 노드에 대해서 탐색을 진행 하며 totalInput값을 계산
    for (auto child : root->links)
    {
        if(child != nullptr)
            PreorderTraverse(child, 1);
    }

    // 계산된 totalInput의 평균을 구하고, 소수 둘째 자리에서 반올림
    float retVal = static_cast<float>(totalInput) / size;
    retVal = round(retVal * 100) / 100;

    return retVal;
}

PreorderTraverse함수의 첫번째 매개변수는 탐색을 할 노드이고, 두 번째 매개변수는 지금까지의 입력값이다. 만약 입력으로 ["hello", "hell", "heaven", "good"]이 주어졌다면 다음과 같이 트라이가 구성될 것이다.

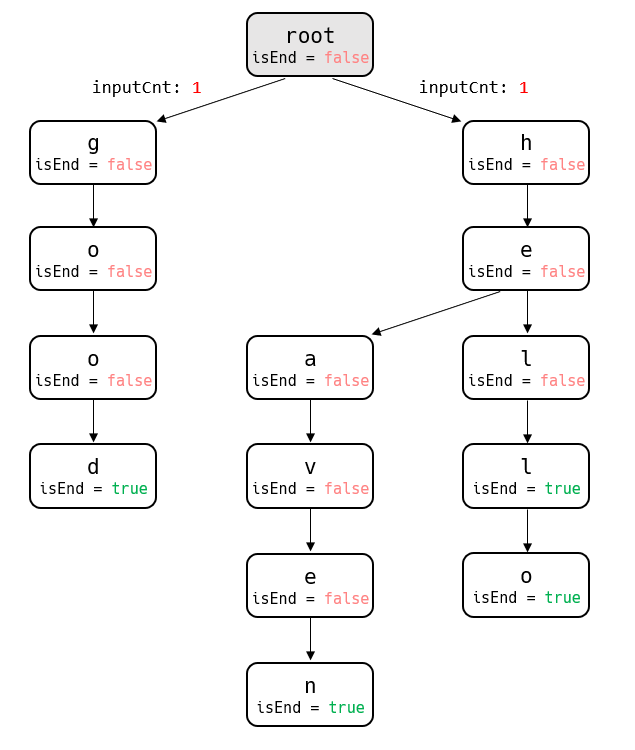
루트 노드의 자식 노드는 h와 g 두 개가 있기 때문에, PreorderTraverse 함수가 두 번 실행될 것이다. 그리고 각각 첫 글자이기 때문에 지금까지 입력값은 1로 전달될 것이다.

다음으로 PreorderTraverse함수 구현에 대해서 생각해 보자. 문자열이 자동 완성되지 않고 입력이 필요한 경우는 두 가지가 존재한다.

  • 자식 노드가 1개 보다 많아서 현재 노드가 분기 노드가 되는 경우
  • 현재 노드가 문장의 완성인 경우

먼저 자식 노드가 1개 보다 많아서 현재 노드가 분기되는 경우를 살펴보자.

자식 노드가 한 개 보다 많은 경우를 살펴보자. "he"까지 입력받았을 때 'e' 노드의 자식 노드는 두 개다. 이곳은 분기점이 되는 노드이기 때문에 유저로부터 새로운 문자를 입력받아야 한다. 때문에 이때 inputCnt를 1 증가시켜준다.

 

다음으로 현재 노드가 문장의 완성인 경우를 살펴보자.

 

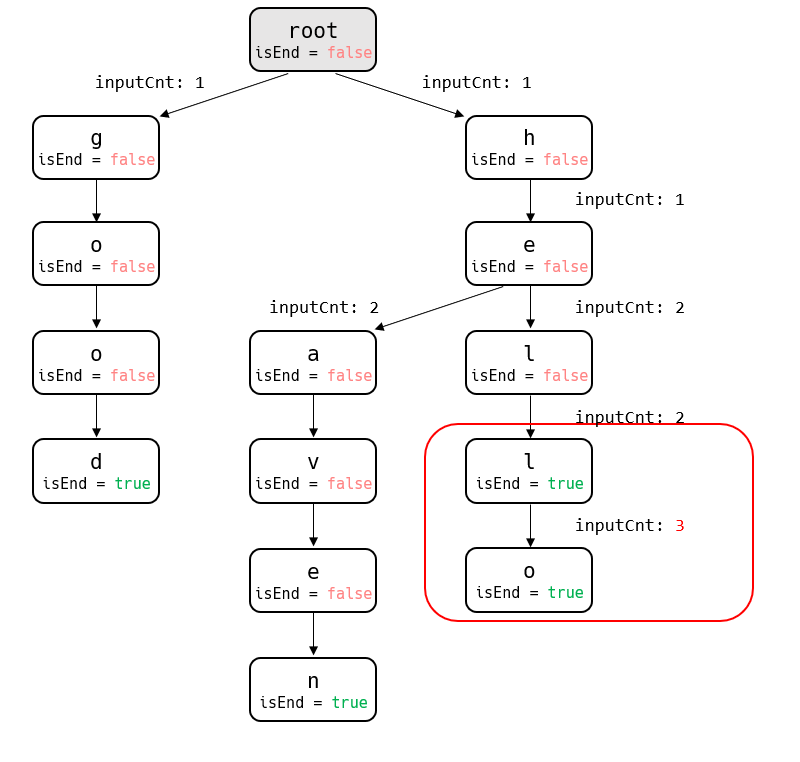
"hell"은 이미 하나의 문장으로 완성되어서 'l' 노드에 isEnd가 true일 것이다. 하지만, "hello"로 넘어가기 위해서는 입력이 한번 더 필요하다. 

 

그리고 최종적으로 isEnd 가 true인 경우 하나의 문장이 완성되었기 때문에 지금까지의 inputCnt를 totalInput에 더해주자. 지금까지의 내용을 코드로 구현하면 다음과 같다.

void Trie::PreorderTraverse(Node* node, int inputCnt)
{
    // 현재 노드가 끝 노드일 때 다음 노드로 가기 위해서는 입력을 하나 더 받아야 한다.
    // 그리고 지금까지의 inputCnt를 totalInput에 더해야 한다.
    if (node->isEnd) {
        totalInput += inputCnt;

        inputCnt++;
    }
    // 자식 노드가 1개보다 많다면, 새로운 입력을 받아야 한다.
    else if (node->numChild > 1)
    {
        inputCnt++;
    }
    else
    {
        // 자식 노드가 한개 && 현재 노드가 isEnd가 아니라면 inputCnt를 증가시키지 않는다.
    }

    // 자식 노드가 있다면 탐색을 더 진행한다.
    for (auto child : node->links)
    {
        if (child != nullptr)
            PreorderTraverse(child, inputCnt);
    }
}

성능 평가

전체 시간 복잡도를 계산해 보자. 먼저 Insert 함수 같은 경우 문자열 길이만큼 반복문을 시행하기 때문에 문자열 길이가 \(m\)이라면 \(O(m)\) 시간 복잡도를 가진다. 그리고 모든 main 함수에서 모든 문자열을 삽입하기 때문에 문자들을 트라이에 삽입하기 위한 총 시간 복잡도는 \(O(m \cdot n)\)이라 할 수 있다. 그리고  Solution 함수는 전위 순회를 통해서 모든 노드에 접근한다. 노드의 개수는 또한 \(m \cdot n\) 이기 때문에 Solution 함수의 복잡도 또한 \(O(m \cdot n)\)이다. 공간 복잡도 또한 모든 노드들은 자식 노드 주소 값 26개를 가지기 때문에 \(O(m \cdot n)\)이라고 할 수 있다.

 

이 문제에서는 시간을 상당히 빠듯하게 주기 때문에 자식 노드의 컨테이너로 unordered_map을 사용하게 될 경우 시간 초과가 발생할 수 있다. 필자의 경우 한 번은 924ms에 통과했고 코드를 살짝 수정했을 때 대부분 시간 초과가 발생했다. 그래서 자식 노드의 컨테이너를 빠른 인덱싱으로 접근 가능한 array로 사용했을 때 664ms까지 시간을 줄일 수 있었다. 대신 array를 사용할 경우 사용되지 않을 공간까지 모두 할당하기 때문에 공간을 조금 더 사용하는 경향이 있다.

 

전체 소스 코드

이번 문제에서는 소멸자를 구현하지 않으면 메모리 릭이 발생할 수 있는 문제이다.  소멸자는 재귀적으로 구현되어 있으니 참고하자.

#include <iostream>
#include <array>
#include <string>
#include <cmath>
#define endl '\n'

using namespace std;

struct Node {
    Node() : isEnd(false), links{}, numChild(0)
    {}

    array<Node*, 26> links;
    bool isEnd;
    int numChild;
    static size_t GetIndex(char ch) { return ch - 'a'; }
};
class Trie {
public:
    Trie() : totalInput(0), size(0) { root = new Node(); }
    ~Trie() { DeleteLinks(root); }
    void Insert(const string& word);
    float Solution();

private:
    void PreorderTraverse(Node* node, int inputCnt);  // 노드 탐색을 위한 재귀함수
    void DeleteLinks(Node* node);   // 전체 노드 삭제를 위한 제귀함수
    Node* root;
    int totalInput; // 자동완성을 위해서 입력해야하는 총 input 수 
    int size;   // 문자열의 개수
};
void Trie::Insert(const string& word)
{
    Node* cur = root;
    for (size_t i = 0; i < word.length(); ++i)
    {
        size_t idx = Node::GetIndex(word[i]);

        if (cur->links[idx] == nullptr)
        {
            cur->links[idx] = new Node();
            cur->numChild++;
        }
        cur = cur->links[idx];
    }
    cur->isEnd = true;
    size++;
}
float Trie::Solution()
{
    totalInput = 0;

    // root 노드의 모든 자식 노드에 대해서 탐색을 진행 하며 totalInput값을 계산
    for (auto child : root->links)
    {
        if(child != nullptr)
            PreorderTraverse(child, 1);
    }

    // 계산된 totalInput의 평균을 구하고, 소수 둘째 자리에서 반올림
    float retVal = static_cast<float>(totalInput) / size;
    retVal = round(retVal * 100) / 100;

    return retVal;
}

void Trie::PreorderTraverse(Node* node, int inputCnt)
{
    // 현재 노드가 끝 노드일 때 다음 노드로 가기 위해서는 입력을 하나 더 받아야 한다.
    // 그리고 지금까지의 inputCnt를 totalInput에 더해야 한다.
    if (node->isEnd) {
        totalInput += inputCnt;

        inputCnt++;
    }
    // 자식 노드가 1개보다 많다면, 새로운 입력을 받아야 한다.
    else if (node->numChild > 1)
    {
        inputCnt++;
    }
    else
    {
        // 자식 노드가 한개 && 현재 노드가 isEnd가 아니라면 inputCnt를 증가시키지 않는다.
    }

    // 자식 노드가 있다면 탐색을 더 진행한다.
    for (auto child : node->links)
    {
        if (child != nullptr)
            PreorderTraverse(child, inputCnt);
    }
}
void Trie::DeleteLinks(Node* node)
{
    for (auto child : node->links)
    {
        if (child != nullptr)
        {
            DeleteLinks(child);
        }
    }
    delete node;
}

int main()
{
    // 입출력 성능 향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);
    // 소수 둘째자리 까지 출력을 위한 설정
    cout.precision(2);
    cout << fixed;

    size_t N;  // 입력 받을 문자열 개수
    while (cin >> N)
    {
        Trie trie;

        for (size_t i = 0; i < N; ++i)
        {
            string word;
            cin >> word;
            trie.Insert(word);
        }
        cout << trie.Solution() << endl;
    }
    return 0;
}

 

댓글 , 엮인글
코딩 레시피
블로그 이미지 dev-sbee 님의 블로그
MENU
CATEGORY
VISITOR 오늘 / 전체

티스토리툴바