전화번호 목록 (Level 2)
문제
코딩테스트 연습 - 전화번호 목록
전화번호부에 적힌 전화번호 중, 한 번호가 다른 번호의 접두어인 경우가 있는지 확인하려 합니다. 전화번호가 다음과 같을 경우, 구조대 전화번호는 영석이의 전화번호의 접두사입니다. 구조
programmers.co.kr
접근법
이 문제는 해시 테이블만 사용하여 풀이한 적이 있다. (해시 테이블만 활용한 기존 풀이 보기) 트라이를 배우고 이 문제를 다시 보니 해시 테이블만 사용했을 때 보다 트라이를 활용했을 때 더 좋은 성능을 낼 수 있을 듯하여 다시 풀었다. 트라이는 여러 문자열들을 입력받아 동일한 접두사를 효율적으로 찾아낼 수 있다는 특징이 있다. 그래서 접두사를 찾아내야 하는 이 문제에 적합한 자료구조가 된다. 트라이 자료구조에 대한 더 자세한 설명은 이 글을 참고하자.
자료구조 정의
먼저 이 문제의 문자열은 숫자로만 이루어져 있다. 그래서 자식 노드는 최대 10개이며, 인덱싱 함수가 간단하기 때문에 배열을 활용하여 자식 노드를 구성해 보려한다. 또한 한 전화번호가 다른 전화번호의 접두사인지 아닌지 파악하기 위해서는 전화번호의 끝을 나타낼 수 있는 isEnd 변수가 필요해 보인다. 따라서 다음과 같이 Node 구조체를 정의한다.
struct Node{
Node() : isEnd (false), links{}
{}
bool isEnd;
array<Node*, 10> links;
static size_t GetIndex(char ch) {return ch - '0';}
};트라이 자료구조를 사용할 때 가장큰 장점은 모든 문자열을 다 삽입하지 않더라도, 문자열을 삽입하는 중간에 접두사인지 아닌지 바로 파악할 수 있다. (기준 해시 테이블만 사용한 풀이에서는 모든 전화번호를 해시 테이블에 삽입 후 하나씩 확인했었다.) 이를 위해서 우리는 문자열 삽입 과정에서 bool 값을 반환할 Insert 함수를 가진 Trie 클래스를 아래와 같이 정의할 수 있다.
class Trie{
public:
Trie() { root = new Node(); }
~Trie() { DeleteAll(root); }
bool Insert (const string& str ); // 삽입 과정에서 유효한 번호인지 판단
private:
Node* root;
void DeleteAll(Node* node); // 모든 노드를 삭제하기 위한 함수. 재귀적으로 구현
};이렇게 구현된 Trie 클래스는 다음과 같이 사용할 예정이다.
bool solution(vector<string> phone_book) {
bool answer = true;
Trie trie;
for(const string& number : phone_book )
{
// 유효하지 않은 전화번호가 삽입되면 false를 반환하고 종료.
if(trie.Insert(number) == false)
return false;
}
// 모든 전화번호가 정상적으로 삽입되었다면 유효한 phone_book 이다.
// tire의 소멸자가 자동으로 호출되면서 동적으로 할당된 노드가 삭제됨.
return true;
}구현
이 문제의 핵심인 Insert 함수를 구현해보자. 아래와 같이 유효한 전화번호부가 있다고 가정하자.
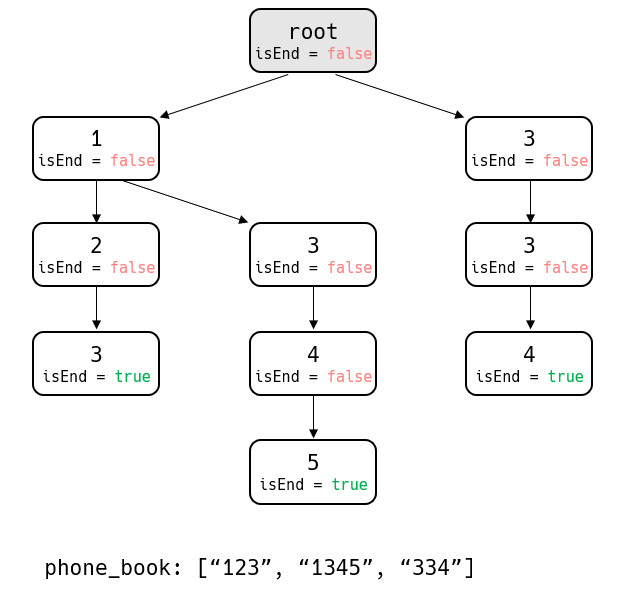
[그림 1]은 한 번호가 다른 번호의 접두사인 경우가 없는 유효한 전화번호부 이다. 여기에 아래와 같이 새로운 번호 "3345"를 삽입해보자.
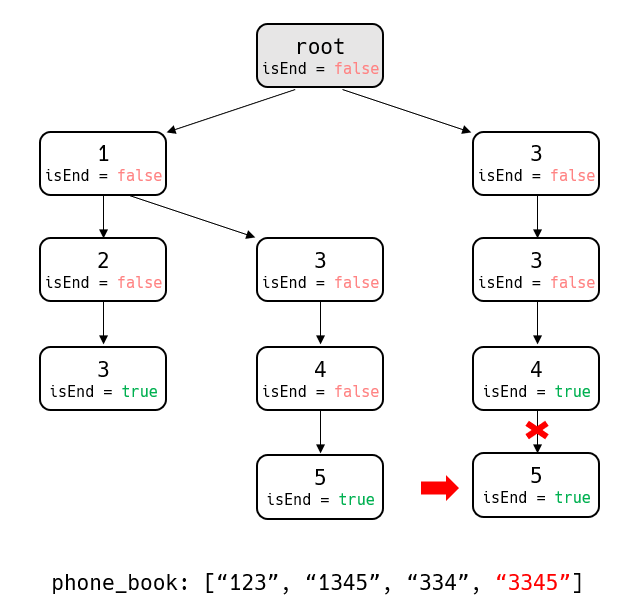
새로운 번호 "3345"는 "334"를 접두사로 가지는 번호이다. "3345"를 삽입하기 위해서는 노드 3→3→4를 지나와야 한다. 그런데 노드 4는 이미 isEnd 가 true로 설정되어 있다. 이번 예시에서 true로 설정된 노드 이후에 새로운 자식 노드가 들어온다면 해당 전화번호가 유효하지 않다는 사실을 알 수 있다. 다른 예시도 살펴보자.
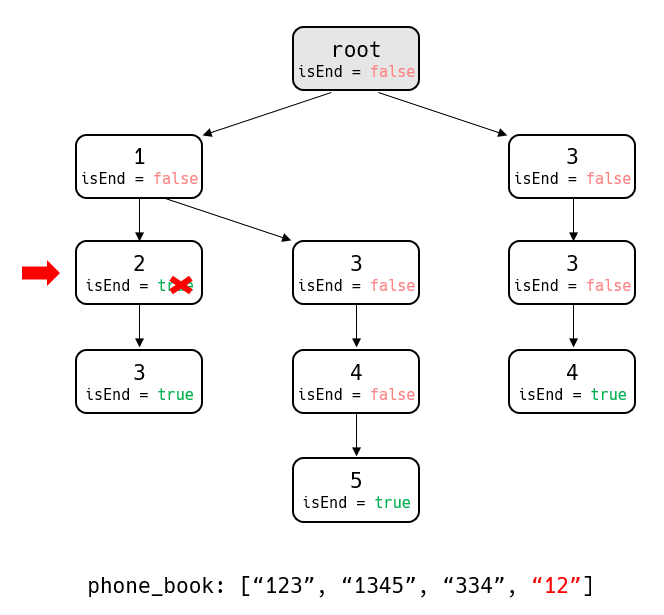
이 번에는[그림 1] 트라이에 전화번호 "12"를 삽입해보자. "12"는 "123"의 접두사이기 때문에 유효할 수 없다. 우리는 "12"를 삽입할 때 노드 "2"의 자식 노드가 있는지 확인할 수 있다. "2"에 자식 노드가 있다면 "12"는 어떠한 번호의 접두사 전화번호가 되기 때문에 이러한 삽입은 유효하지 않다는 것을 알 수 있다. 따라서 일반적인 트라이 노드 삽입 함수에 [그림 2], [그림 3]과 같은 상황에는 false를 반환도록 Insert 함수를 구현할 수 있을 것이다.
bool Trie::Insert(const string& str)
{
Node* cur = root;
// 반복문 시간 복잡도 (O(1))
for(size_t i = 0; i < str.length(); ++i)
{
// 그림 2의 경우 (cur노드에 새 자식 노드를 추가하는데 해당 노드가 잎 노드인 경우)
if(cur->isEnd == true)
return false;
size_t index = Node::GetIndex(str[i]);
if(cur->links[index] == nullptr)
{
cur->links[index] = new Node();
}
cur = cur->links[index];
}
cur->isEnd = true;
// 그림 3의 경우 (노드 삽입 후 자식 노드가 존재하는지 확인)
for(Node* child : cur->links)
{
if(child != nullptr)
return false;
}
return true;
}Insert 함수의 시간 복잡도를 살펴보자. Insert 함수의 시간 복잡도는 \(O(1)\)이다. 비록 반복문이 있지만, 전화번호의 최대 길이는 20이기 때문에 최악의 경우에도 반복문은 20회만 동작하기 때문에 \(O(1)\)로 볼 수 있다.
성능 평가
가장 시간 복잡도가 높은 함수인 Insert 함수의 시간 복잡도가 무려 \(O(1)\)이다. 때문에 모든 노드를 삽입하더라도 최악의 경우에도 \(O(n)\)만에 연산을 마칠 수 있다. 기존 해시테이블만 사용한 풀이한 코드의 시간 복잡도 또한 \(O(n)\)으로 트라이를 사용한 풀이와 동일하다. 하지만 기존 풀이에서 아래의 부분을 살펴보자.
for(auto number : phone_book) // 모든 전화번호에 대해서
for(int i = 1; i < number.length(); i++) // 모든 경우의 수에 대해서 (자기자신 제외)
if(ht.find(number.substr(0,i)) != ht.end()) // 중복된 번호가 있다면 false
return false;해시 테이블의 find 함수의 시간 복잡도는 \(O(1)\)이지만 연산량이 적지 않다. 더욱이 문자열이 길어질수록 성능은 매우 떨어지게 된다. 또한 substr 함수도 문자열 길이만큼의 시간 복잡도를 가진다. 결국 해당 반복문은 \(O(t^2 \cdot n)\) 시간 복잡도를 가지게 된 셈이다. 문자열의 최대 길이가 20으로 한정되어 있어 사용할수 없을 만큼 느린것은 아니지만 이번 트라이를 활용한 풀이에 비하면 다소 느리다고 할 수 있다. 이번 트라이 풀이에서 사용한 배열의 GetIndex 함수의 연산은 오직 뺄셈연산 하나로 이루어져 있기 때문이다. 그래서 같은 \(O(1)\) 시간 복잡도를 가졌지만 아래 그림 4와 같이 2~5배가량의 성능 차이를 보이게 된다.
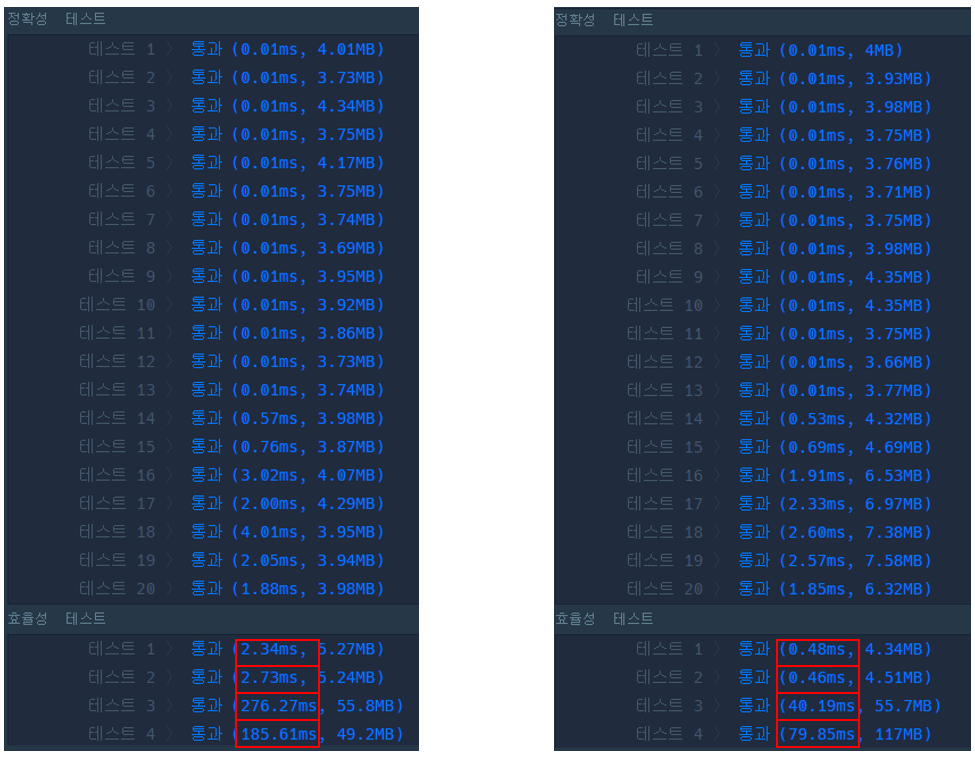
하지만, 공간 복잡도에서는 두 경우 모두 \(O(n)\)이지만 항상 모든 노드에 자식노드 포인터 배열을 10개씩 가져야 하는 트라이 구조보다 필요한 만큼 문자열을 동적으로 가지는 해시 테이블이 조금 더 효율적임을 확인할 수 있다.
전체 코드
동적으로 할당한 노드를 모두 해제하는 소멸자 코드는 재귀적으로 구현되어 있음에 주의하자.
// 문제 : 전화번호 목록 (Level 2)
// 출처 : 프로그래머스 (https://programmers.co.kr/learn/courses/30/lessons/42577)
// 풀이 : https://dev-sbee.tistory.com/ 참고
#include <string>
#include <vector>
#include <array>
using namespace std;
struct Node{
Node() : isEnd (false), links{}
{}
bool isEnd;
array<Node*, 10> links;
static size_t GetIndex(char ch) {return ch - '0';}
};
class Trie{
public:
Trie() { root = new Node(); }
~Trie() { DeleteAll(root); }
bool Insert (const string& str ); // 삽입 과정에서 유효한 번호인지 판단
private:
Node* root;
void DeleteAll(Node* node); // 모든 노드를 삭제하기 위한 함수. 재귀적으로 구현
};
bool Trie::Insert(const string& str)
{
Node* cur = root;
// 반복문 시간 복잡도 (O(1))
for(size_t i = 0; i < str.length(); ++i)
{
// 그림 2의 경우 (새 노드를 추가해야하는데 해당 노드가 잎 노드인 경우)
if(cur->isEnd == true)
return false;
size_t index = Node::GetIndex(str[i]);
if(cur->links[index] == nullptr)
{
cur->links[index] = new Node();
}
cur = cur->links[index];
}
cur->isEnd = true;
// 그림 2의 경우 (자식 노드가 존재하는지 확인)
for(Node* child : cur->links)
{
if(child != nullptr)
return false;
}
return true;
}
void Trie::DeleteAll(Node* node)
{
for(Node* child : node->links)
{
if(child != nullptr)
DeleteAll(child);
}
delete node;
}
bool solution(vector<string> phone_book) {
bool answer = true;
Trie trie;
for(const string& number : phone_book )
{
// 유효하지 않은 전화번호가 삽입되면 false를 반환하고 종료.
if(trie.Insert(number) == false)
return false;
}
// 모든 전화번호가 정상적으로 삽입되었다면 유효한 phone_book 이다.
// tire의 소멸자가 자동으로 호출되면서 동적으로 할당된 노드가 삭제됨.
return true;
}