개미굴(골드 II)
문제
14725번: 개미굴
첫 번째 줄은 로봇 개미가 각 층을 따라 내려오면서 알게 된 먹이의 정보 개수 N개가 주어진다. (1 ≤ N ≤ 1000) 두 번째 줄부터 N+1 번째 줄까지, 각 줄의 시작은 로봇 개미 한마리가 보내준 먹이
www.acmicpc.net
접근법
트라이 자료구조를 이해하기 위해서 풀어본 문제이다. 트라이에 기본적인 설명은 이 글을 참고하자. 일반적으로 트라이라 하면 접두사를 검색하거나 단어를 검색하기 위해서 많이 사용된다. 그런데 이 문제에서는 하나의 노드에 하나의 단어가 들어가는 구조로 변형하여 사용한다는 특징이 있다.
자식 노드 개수에 제한이 없기 때문에 자식 노드의 포인터들을 배열처럼 정적인 공간에 담을 수는 없다. 그리고 여러 자식 노드들 중에서 사전 순으로 빠른 단어가 먼저 출력되어야 한다. 때문에 unordered_map 보다는 map을 선택함이 바람직하다. (map의 Insert 함수는 \(O(\mbox{log}n)\) 시간 복잡도를 가졌음을 유의하자)
그리고 항상 트리의 마지막 까지 탐색이 진행되고 탐색 중간에 문장이 완성되는 경우는 없다. 때문에 isEnd와 같은 boolean 변수도 필요 없어 보인다. 왜냐하면 자식 노드가 비었다는 사실로 그 노드가 잎 노드임을 알 수 있다. 따라서 Node 구조체와 Trie 클래스를 다음과 같이 선언할 수 있다.
struct Node {
Node() {}
map<string, Node*> links;
};class Trie {
public:
Trie() { root = new Node(); }; // root 노드를 생성을 잊지 말자.
~Trie() { PostorderTraverse(root); };
void Insert(const vector<string>& words); // 하나의 로봇 개미의 신호를 매개변수로 받아 Trie를 만든다.
void PrintAll(); // 문제 조건에 맞게 전위 순회를 활용한 출력함수
private:
Node* root;
// 출력을 위한 전위 순회
void PreorderTraverse(const string& word, Node* node, int depth);
// delete를 위한 후위 순회
void PostorderTraverse(Node* node);
};구현
main 함수
트라이 자료구조를 어떻게 활용할 계획인지 main 함수를 먼저 살펴보자.
int main() {
int N; // 먹이 정보 개수 (1 <= N <= 1,000)
int K; // 로봇 개미 한 마리가 보내준 최대 먹이 정보의 개수 (트리의 깊이) (1<= K <= 15)
vector<string> words; // 하나의 로봇 개미가 보내준 신호를 전달받을 문자열 벡터
words.reserve(15);
Trie trie;
cin >> N;
for (int i = 0; i < N; ++i)
{
cin >> K;
for (int j = 0; j < K; ++j)
{
string word;
cin >> word;
words.emplace_back(word);
}
trie.Insert(words);
words.clear();
}
trie.PrintAll();
return 0;
}먼저 하나의 개미가 보내준 신호를 words 변수에 담고, 앞으로 구현할 트라이의 Insert멤버 함수에 입력한다. 이 작업을 N번 반복한 후 완성된 개미굴 지형을 앞으로 구현할 트라이의 PrintAll 멤버함수로 출력한다. 이 두 함수 모두 이론적으로는 Iterative 한 방법과 Recursive 한 방법으로 구현할 수 있지만, 구현의 편의상 Insert는 Iterative한 방식으로 PrintAll 함수는 Recursive 한 방식으로 구현하였다. (동적 생성한 노드를 삭제할 소멸자는 Recursive 한 방식으로 구현했다.)
Trie::Insert 함수
먼저 Insert함수를 살펴보자.
void Trie::Insert(const vector<string>& words)
{
Node* cur{ root };
// 반복문 시간 복잡도: O(K * t * log N)
for (size_t i = 0; i < words.size(); ++i)
{
if (cur->links.find(words[i]) == cur->links.end())
{
// Insert 시간 복잡도: O(t * log N)
cur->links[words[i]] = new Node();
}
cur = cur->links[words[i]];
}
}자식 노드에 이미 노드가 들어왔을 수 있다. 예를 들어 다음과 같이 입력이 들어오는 경우를 살펴보자.
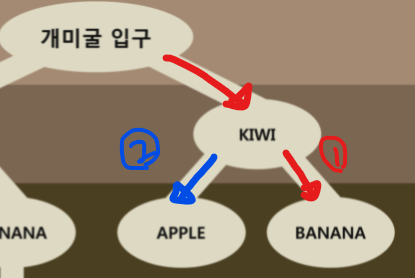
KIWI BANANA
KIWI APPLE
첫 번째 입력이 되었을 때는 root 노드의 자식노드에 KIWI가 없기 때문에 새 노드를 생성했을 것이다. 두 번째 입력에서는 root 노드의 자식 노드에 KIWI가 존재하기 때문에 조건문을 들어가지 않고 현재 노드 포인터에 KIWI노드를 대입하여 더 아래로 내려갈 수 있다.
시간 복잡도를 살펴보자. 만약 N 번의 로봇 개미가 신호를 보냈는데 모두 다른 노드를 보냈다면 자식 노드의 개수는 최대 N가 까지 증가할 수 있다. map은 이진 트리를 사용하기 때문에 하나의 노드를 삽입하기 위해서는 \(O(\mbox{log} N)\) 시간 복잡도를 가질 것이다. 하지만 여기서 map의 요소는 문자열이다. 삽입을 위해 비교연산을 하기 위해서는 문자열의 모든 문자를 비교해야 하기 때문에 문자열 길이 t만큼의 시간이 더 소요된다. 때문에 map에 삽입하는 연산의 시간 복잡도는 \(O( t \cdot\mbox{log} N)\)이다. 그리고 words.size()는 로봇 개미 한 마리가 보내준 먹이 정보 개수 K를 뜻한다. 따라서 Trie::Insert 함수의 시간 복잡도는 \( O(K \cdot t \cdot\mbox{log} N)\) 이다.
Trie::PrintAll 함수
다음으로 모든 출력을 위한 Trie::PrintAll 함수를 살펴보자.
void Trie::PrintAll()
{
for (auto link : root->links)
{
PreorderTraverse(link.first, link.second, 0);
}
}PrintAll 함수에서는 간단하게 root 노드의 모든 자식 노드들에 대해서 전위 순회를 하며 출력하도록 하였다.
void Trie::PreorderTraverse(const string& word, Node* node, int depth)
{
// 반복문 시간 복잡도 O ( K )
for (int i = 0; i < depth; i++)
{
cout << "--";
}
cout << word << endl;
for (auto link : node->links)
{
PreorderTraverse(link.first, link.second, depth + 1);
}
}전위 순회를 통해서 현재 노드를 출력한 후 모든 자식노드를 순서대로 순회한다. "--"를 출력하기 위한 반복문은 \(O(K)\)이며 전위 순회는 모든 노드에 대해서 진행되고 모든 노드의 개수는 최대 K * N 이기 때문에 Trie::PrintAll 함수의 최종 시간 복잡도는 \(O(K^2 \cdot N)\)가 될 것이다.
(소멸자 부분 코드는 아래의 전체 코드를 참고하자.)
성능 평가
Trie::PrintAll 함수의 최종 시간 복잡도는 \(O(K^2 \cdot N)\) 이지만, Trie::Insert 함수의 시간 복잡되는 \( O(K \cdot t \cdot\mbox{log} N)\)이고 Trie::Insert 함수는 main 함수에서 N번 호출된다. 따라서 이 알고리즘의 최종 시간 복잡도는 \( O(K \cdot t \cdot N \cdot \mbox{log} N)\) 그런데 K와 t는 최대 15이기 때문에 무시할 수 있는 정도여서 최종 적으로는 \( O(N \cdot \mbox{log} N)\) 이라고도 할 수 있다.
공간 복잡도의 경우 전체 노드의 개수는 K * N 이며 각 노드마다 길이 t인 문자열을 가지고 있기 때문에 공간 복잡도는 \(O(t \cdot k \cdot N)\)이 된다. 하지만 여기서도 K와 t값을 무시한다면 최종 공간 복잡도는 \(O(N)\)이 된다. 테스트 결과 다음과 같이 무난하게 통과할 수 있었다.

전체 코드
#include <string>
#include <vector>
#include <iostream>
#include <map>
using namespace std;
struct Node {
Node() {}
map<string, Node*> links;
};
class Trie {
public:
Trie() { root = new Node(); }; // root 노드를 생성을 잊지 말자.
~Trie() { PostorderTraverse(root); };
void Insert(const vector<string>& words); // 하나의 로봇 개미의 신호를 매개변수로 받아 Trie를 만든다.
void PrintAll(); // 문제 조건에 맞게 전위 순회를 활용한 출력함수
private:
Node* root;
// 출력을 위한 전위 순회
void PreorderTraverse(const string& word, Node* node, int depth);
// delete를 위한 후위 순회
void PostorderTraverse(Node* node);
};
void Trie::Insert(const vector<string>& words)
{
Node* cur{ root };
// 반복문 시간 복잡도: O(K * t * log N)
for (size_t i = 0; i < words.size(); ++i)
{
if (cur->links.find(words[i]) == cur->links.end())
{
// Insert 시간 복잡도: O(t * log N)
cur->links[words[i]] = new Node();
}
cur = cur->links[words[i]];
}
}
void Trie::PrintAll()
{
// 반복문 시간 복잡도 O (K^2 * N)
for (auto link : root->links)
{
PreorderTraverse(link.first, link.second, 0);
}
}
void Trie::PreorderTraverse(const string& word, Node* node, int depth)
{
// 반복문 시간 복잡도 O ( K )
for (int i = 0; i < depth; i++)
{
cout << "--";
}
cout << word << endl;
for (auto link : node->links)
{
PreorderTraverse(link.first, link.second, depth + 1);
}
}
void Trie::PostorderTraverse(Node* node)
{
for (auto link : node->links)
{
PostorderTraverse(link.second);
}
delete node;
}
int main() {
// 입출력 성능 향상을 위한 설정
ios_base::sync_with_stdio(false);
cout.tie(NULL);
cin.tie(NULL);
int N; // 먹이 정보 개수 (1 <= N <= 1,000)
int K; // 로봇 개미 한 마리가 보내준 최대 먹이 정보의 개수 (트리의 깊이) (1<= K <= 15)
vector<string> words;
words.reserve(15);
Trie trie;
cin >> N;
// 전체 데이터 입력 시간 복잡도
// O(K * t * N * log N)
for (int i = 0; i < N; ++i)
{
cin >> K;
for (int j = 0; j < K; ++j)
{
string word;
cin >> word;
words.emplace_back(word);
}
// Insert의 시간 복잡도 (O(K * t * log N))
trie.Insert(words);
words.clear();
}
trie.PrintAll();
return 0;
}
