[프로그래머스] (동적계획법) 도둑질 (C++)

도둑질 (Level 4)

문제

전체 문제 보기

코딩테스트 연습 - 도둑질

접근법

이 문제에서 구해야 하는 값은 "각 집에 있는 돈이 담긴 배열 money가 주어질 때, 도둑이 훔칠 수 있는 돈의 최댓값"이다. 답을 구하기 위해서 우리가 고려해야 할 점들을 살펴보자.

• 연속해서 두 집은 털 수 없다.
• 집들이 원형으로 순환되어 배치되어있다. 그래서 첫 번째 집을 털었다면 마지막 집은 털 수 없다.

우선 첫 번째 조건을 고려하여 알고리즘을 설계하고 두 번째 조건을 만족시키기 위해 설계된 알고리즘을 개선하도록 한다.

 

1단계. 점화식 설계

먼저 연속한 두 집은 털 수 없다는 조건 하에서 \(n\) 번째 집에서 돈의 최댓값을 구해보자. 우리는 돈의 최댓값만 구하는 것이지, 털어야 할 집이 어딘지는 구할 필요가 없다는 것을 상기하자. 아래와 같이 \(n\)개의 집이 있다고 가정하자.

 [1] [2] [3] ... [n-2] [n-1] [n]

우리가 \(n\)개의 집을 털었을 때 최댓값을 구하기 위해서는 \(n\)번째 집을 털어야 할지 \(n\)번째 집을 털지 말아야 최댓값이 될지 알아야 한다.

만약 \(n\)번재 집에 돈이 굉장히 많다면, \(n-1\)번째 집을 터는 것을 포기하더라도 \(n\)번째 집을 털어야 할 것이다. 그런데 \(n\)번째 집에 돈이 별로 없고 \(n-1\)에 돈이 많다면 \(n\)번째 집을 포기할 수도 있을 것이다. 즉, \(n\)번째 집을 털지 말지를 결정할 알고리즘이 필요하다.

 

n번째 집을 털지 말지를 결정하기 위해서 단순히 \(n-1\)번째 집과 \(n\) 번째 집을 비교하는 것 만으로는 부족하다. 만약 \(n-2\)에 돈이 엄청 많다면, \(n-1\)을 포기하고 \(n-2\)를 털고 \(n\)을 터는 선택을 할 수도 있기 때문이다. 즉 과거의 모든 선택들이 \(n\)번째 선택에 영향을 주게 된다. 그렇기 때문에 우리는 과거의 선택까지 포괄할 수 있는 기준이 필요하다.

 

\(n\) 번째 집까지 고려했을 때 훔칠 수 있는 돈의 최댓값을 \(f(n)\), \(n\)번째 집의 돈이 \(m(n)\)이라고 하자. 그렇다면 우리가 고려해야 하는 것은 \(n-1\) 번째 혹은 \(n-2\) 번째 집의 돈 \(m(n-1)\) 이나 \(m(n-2)\)가 아니라, \(n-1\)까지의 누적금액 \(f(n-1)\)과 \(n-2\)까지의 누적금액 \(f(n-2)\)이다.  만약 \(n\)번째 집의 돈을 훔치려면 "\(n-2\) 번째 집까지 훔친 돈인 \(f(n-2)\) 에 \(m(n)\) 값을 더한 값이 된다."

 

\[f(n) = f(n-2) + m(n)\]

 

반면 \(f(n-1)\)이 충분히 크다면 \(m(n)\)은 포기할 수도 있다. 이 경우의 식은 다음과 같을 것이다.

 

\[f(n) = f(n-1)\]

 

정리하면 점화식은 다음과 같을 것이다.

 

\[f(n) = \mbox{max} \begin{cases} f(n-2) + m(n) \\ f(n-1) \end{cases} \]

 

2단계. 첫 번째집에 대한 선택

이 문제는 그림처럼 집이 순환하기 때문에 첫 번째 집을 털었다면 마지막 집을 털 수 없다. 

▲ 첫 번째 집을 털었기 때문에 마지막집(보라색)은 털 수 없다.

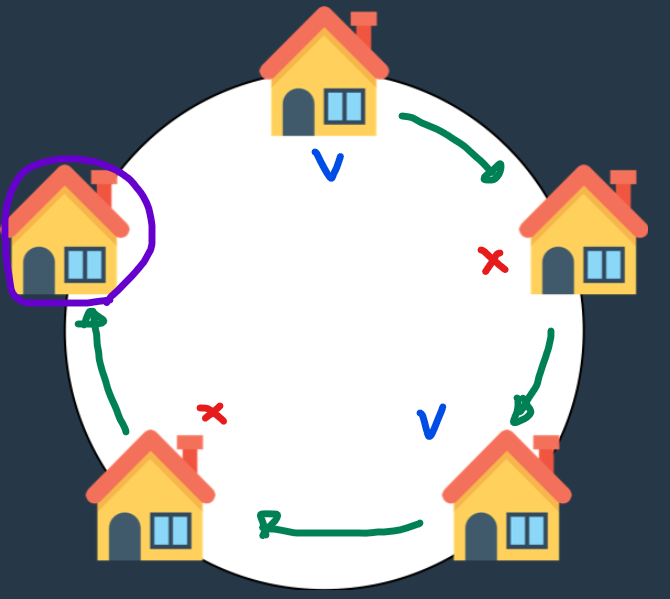
때문에 앞선 점화식에서 마지막 집을 터는 경우인 \(f(n-2) + m(n)\)의 \(f(n-2)\)는 첫 번째 집이 포함되지 않음을 보장해주지 않는다. 때문에 우리는 첫 번째 집이 포함되지 않는 경우를 보장하는 별도의 경우를 고려해야 한다.  \(f(n)\) 점화식을 활용하여 첫 번째 집을 포함하지 않는 \(f_0(n)\) 과 첫 번째 집을 포함하는 \(f_1(n)\) 를 별도로 계산해야 한다.

그리고 최종적으로 n이 마지막인 \((n = last)\) 번째 집에서는 다음의 계산으로 최댓값을 구할 수 있다. 

 

\[f(last) = \mbox{max} \begin{cases} f_0(last-2) + m(last) \\ f_1(last-1) \end{cases} \]

 

구현

동적 계획법은 한번 계산한 결과를 저장하여 불필요한 계산을 줄여 효율을 높이는 방법이다. 이 점화식을 따를 경우 \(f(n-1), f(n-2), f(n-3), ... ,f(1)\)의 값에 대한 호출이 빈번하다. 그래서 한번 계산된 값들은 저장하여 반복되지 않도록 하는 것이 중요하다. 이를 위해서 다음과 같이 Cache 배열을 선언하였다. Cache[0]은 첫 번째 집을 제외한 경우 즉 \(f_0(n)\)을 뜻하고, Cache[1]은 첫 번째 집도 포함된 경우 \(f_1(n)\)을 뜻한다. 아래의 구현은 동적 계획법 중 바텀업 방식을 활용하여 구현하였다.

#include <string>
#include <vector>

using namespace std;

int solution(vector<int> money) {
    int answer = 0;
    int last = money.size() - 1;
    
    // Cache[0]: 첫 번째 집 제외
    // Cache[1]: 첫 번째 집 포함
    int Cache[2][1'000'000];
    
    // 첫 번째 집 제외
    Cache[0][0] = 0;
    Cache[0][1] = money[1];
    
    // 첫 번째 집 포함
    Cache[1][0] = money[0];
    Cache[1][1] = max(money[1], money[0]);
    
    for(int i = 2; i < last; i++ )
    {
        Cache[0][i] = max(Cache[0][i-2] + money[i], Cache[0][i-1]);
        Cache[1][i] = max(Cache[1][i-2] + money[i], Cache[1][i-1]);
    }
    
    // 첫 번째 집 미포함 한 Cache(n-2) + money(n)
    // 첫 번째 집 포함 한 Cache(n-1)
    answer = max(Cache[0][last - 2] + money[last], Cache[1][last - 1]);
    return answer;
}