[프로그래머스] (동적계획법) 등굣길 (C++)

등굣길 (Level 3)

문제

전체 문제 보기

코딩테스트 연습 - 등굣길

접근법

문제의 답을 구하기 위해서 먼저 일반화할 수 있는 규칙을 살펴보자. 격자 모양의 등굣길에서 임의의 점 (m, n)까지 갈 수 있는 최단경로의 개수는 어떻게 구할 수 있을까? 아래의 그림처럼 일반 적으로는 (m, n)으로 가는 경로는 (m-1, n)에서 오는 경로와 (m, n-1)에서 오는 두 가지의 경로뿐이다. 때문에 (m, n)으로 가는 최단 경로의 개수는 결국 (m-1, n)까지의 최단경로와 (m, n-1)까지의 최단 경로의 합이다.

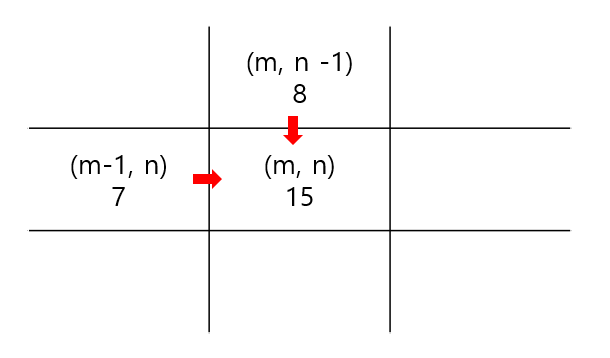
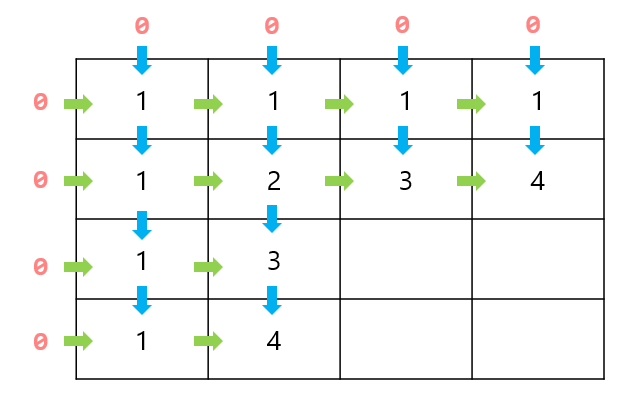
그리고 여기에는 몇 가지 예외가 존재한다. m 또는 n이 1인 경우를 살펴보자. m또는 n이 1인 경우 (m, n)으로 오는 경로는 한쪽 경로밖에 존재하지 않는다. 때문에 한쪽 경로의 값을 그대로 가져온다. 그런데, 이 예외는 일반화 공식에 포함시킬 수 있는 방법이 있다. m 또는 n이 0인 경우의 경로의 값을 0으로 하는 방법이다. 그렇게 될 경우 0은 더해도 값의 변화가 없기 때문에 한쪽 경로의 값을 그대로 가져온 것과 동일한 결과가 나온다. 단 시작 위치(집의 위치)를 1로 설정하기만 하면 쉽게 일반화할 수 있다.

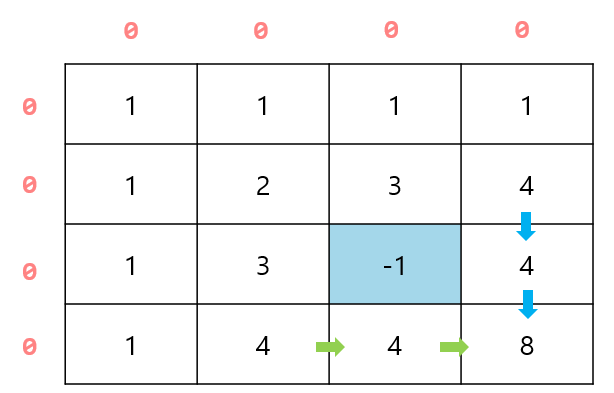
그다음으로 고려해야 할 예외는 물 웅덩이이다. (m-1, n) 혹은 (m, n-1)에 물 웅덩이가 있는 경우 물 웅덩이가 없는 방향의 값을 그대로 가져온다. (여기서는 물 웅덩이를 -1로 지정했다.)

정리하면 다음과 같은 점화식을 세울 수 있다.
\[f(m,n)= \begin{cases} f(m-1,n), & \mbox{if } f(m, n-1) = -1 \\ f(m,n-1), & \mbox{else if } f(m-1, n) = -1 \\f(m-1,n) + f(m, n-1), & \mbox{else } \end{cases}\]

구현

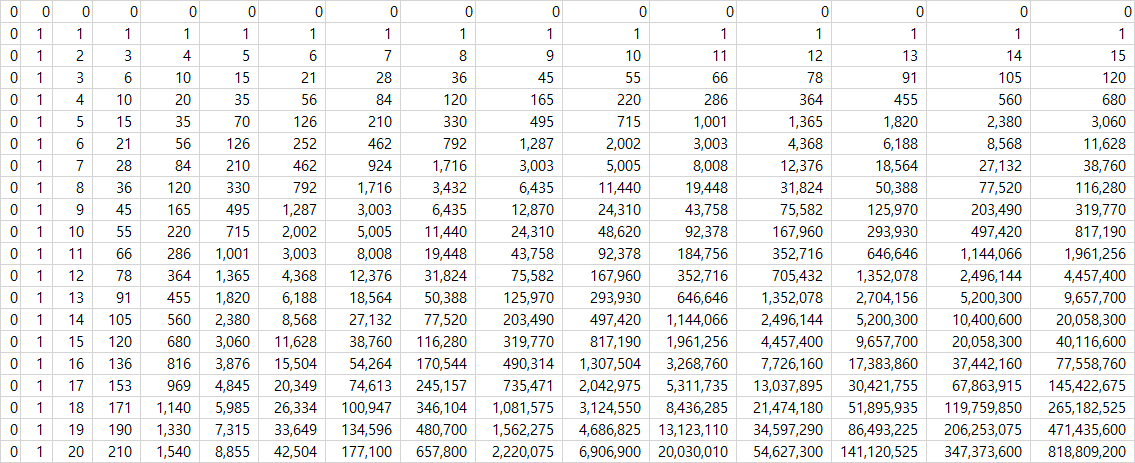
위 식을 구현함에 있어서 주의해야 할 점이 있다. m과 n의 크기가 커짐에 따라 f(m, n)의 크기는 기하급수적으로 커질 수 있다. 아래는 m = 15, n=20 인 경우 나올 수 있는 값의 최댓값들을 엑셀로 계산한 결과이다. 문제에 m과 n의 최댓값은 100이기 때문에 계산과정에서 오버플로가 발생할 수 있다.

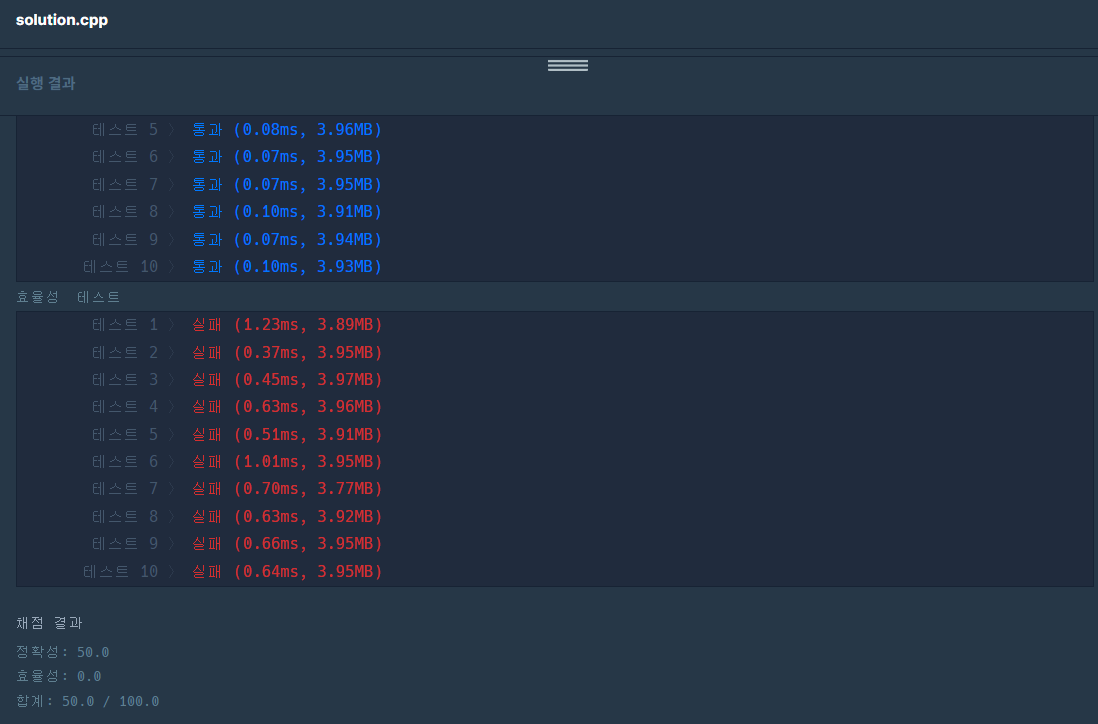
문제에서는 오버플로를 방지하기 위해 계산 결과에 1,000,000,007로 나눈 나머지를 구하도록 하고 있다. 그렇다고 최종 결괏값에 1,000,000,007를 나누면, 계산과정에서 발생할 수 있는 오버플로는 처리할 수 없기 때문에 원하는 결괏값을 얻을 수 없다. 만약 오버플로가 발생한다면 아래의 이미지처럼 정확성 테스트에서는 모두 통과하지만 효율성 테스트에서는 모두 오답이 발생한다.

나머지 연산은 교환 법칙이 성립한다.

\[A % n + B % n = (A + B) % n \]

때문에 아래의 코드처럼 계산 중간 과정에서 오버플로가 발생하지 않도록 1,000,000,007로 나눈 나머지를 사용하도록 하자.

#include <string>
#include <vector>
#include <array> 
using namespace std;

int solution(int m, int n, vector<vector<int>> puddles) {
    int answer = 0;
    array<array<int, 101>, 101> dp {};

    // 물 웅덩이 설정
    for(auto& puddle : puddles)
    {
        dp[puddle[0]][puddle[1]] = -1;
    }

    // 출발지 설정
    dp[1][1] = 1;

    // bottom-up 방식 DP
    for(int i = 1; i <= n; i++ )
    {
        for(int j = 1; j <= m; j++)
        {
            // (j,i)가 물 웅덩이인 경우
            if(dp[j][i] == -1)
                continue;

            // (j-1, i)가 물 웅덩이인 경우
            if(dp[j-1][i] != -1)
                dp[j][i] += dp[j-1][i];

            // (j, i-1)가 물 웅덩이인 경우
            if(dp[j][i-1] != -1)
                dp[j][i] += dp[j][i-1];

            dp[j][i] %= 1'000'000'007;
        }
    }
    // 정답 출력
    answer = dp[m][n];

    return answer;
}