[프로그래머스](Graph) 순위(C++)

순위(Level 3)

문제

전체 문제 보기

코딩테스트 연습 - 순위

접근법

 

이 문제에서 구해야 하는 것은 순위를 알수 없는 선수의 숫자이다.  문제에서 주어진 예시를 그래프와 표로 나타내면 다음과 같다.

▲ 예시의 초기값

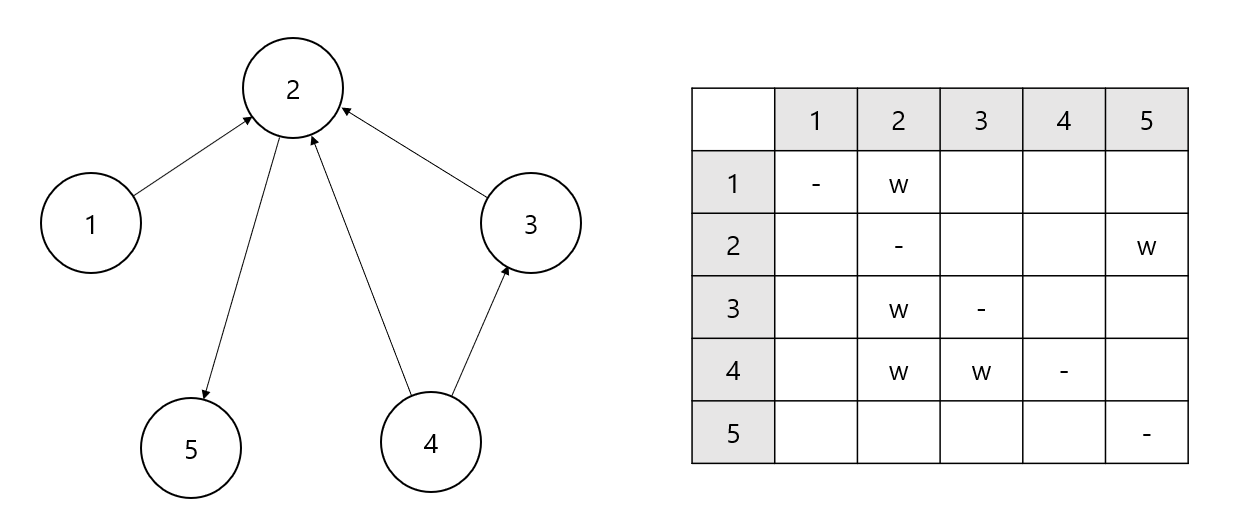
문제의 제한사항을 보면 A선수가 B 선수보다 실력이 좋으면 항상 A선수가 이긴다고 했다. 즉 A선수가 B를 이기고, B선수가 C선수를 이긴다면 A선수는 항상 C 선수를 이긴다는 뜻이다. 이러한 규칙으로 위 그래프에서 추론할 수 있는 경기 결과를 정리해보면 다음과 같을 것이다. 

▲ 경기 결과를 추측한 결과 모습

• 1은 2를 이겼고, 2는 5를 이겼기 때문에 1은 5를 이길 것이다. 
• 4는 2를 이겼고, 2는 5를 이겼기 때문에 4는 5를 이길 것이다.
• 3은 2를 이겼고, 2는 5를 이겼기 때문에 3은 5를 이길 것이다.

2번 선수와 5번 선수를 살펴보자.

• 5번은 나머지 4명의 선수에게 졌기 때문에 5위로 순위가 확실하다.
• 2번은 5번에게만 이기고 모두 졌기 때문에 4위로 순위가 확실하다.

하지만 1, 3, 4번 선수들은 경기 결과가 부족하여 순위를 알 수 없다. 순위를 알수 있는 선수와 알 수 없는 선수의 기준을 정량적으로 표현해보자. 2, 5번 노드는 연결된 엣지가 4개이다. 하지만 1,3,4 노드는 연결된 엣지가 4개 보다 적다. 경기 결과가 부족하여 순위를 알 수  없다는 뜻이다. 즉, n개의 노드에 연결가능한 모든 엣지를 연결했을 때 (노드로 들어오는 엣지의 수) + (노드에서 나가는 엣지의 수) =  (n-1) 인 노드는 순위를 알 수 있고, n-1 보다 적은 노드는 순위를 확정지을 수 없다. 그래서 이 문제를 풀기 위해서는 모든 노드에, 연결 가능한 모든 경로를 연결해줄 수 있는 알고리즘이 필요하다. 그래서 사용할 알고리즘이 플로이드 와샬 알고리즘이다.

 

플로이드 와샬 알고리즘은 일반 적으로 모든 노드간 연결될 수 있는 최단 거리를 계산하는 알고리즘이다. 한 노드에서 출발해서 목표 노드까지의 최단거리를 구하는 다익스트라 알고리즘과 다르게 플로이드 와샬 알고리즘은 연결 가능한 모든 노드사이의 최단거리를 계산한다는 차이가 있다. 연결 가능한 모든 경로를 계산하기 때문에 계산량이 $O(n^3)$인 시간복잡도가 매우 높은 알고리즘이다. 그래서 플로이드 와샬 알고리즘으로 풀어야 하는 문제는 노드의 개수가 적다는 특징이 있다. 이 문제에서 주어진 최대 노드(선수)의 수는 100개 이므로 충분히 플로이드 와샬 알고리즘을 사용할 수 있다.

구현

#include <string>
#include <vector>
#include <iostream>

using namespace std;

int solution(int n, vector<vector<int>> results) {
    int answer = 0;

    vector<vector<bool>> table(n+1, vector<bool> (n + 1, false));
    
    // 경기 결과 승패 기록을 담은 2차원 table에 입력
    // 경기 결과가 존재하는 경우에 true로 마킹
    for(int i = 0; i < results.size(); i ++)
    {
        int winer = results[i][0];
        int loser = results[i][1];
        table[winer][loser] = true;
    }   
    
    // 플로이드 워셜 알고리즘을 통해서 연결 가능한 모든 노드를 true로 마킹
    for(int k = 1; k < n + 1; k++)
        for(int i = 1; i < n + 1; i++)
            for(int j = 1 ; j < n + 1; j++)
            {
                if(table[i][k] && table[k][j])
                    table[i][j] = true;
            }
    
    // 들어오는 엣지와 나가는 엣지의 개수를 카운트하여 순위를 매길 수 없는 선수의 수를 계산
    for(int i = 1; i < n + 1; i++)
    {
        int cnt = 0;
        for(int j = 1; j < n + 1; j++)
        {
            if(table[i][j] || table[j][i])
                cnt++;
        }
        
        //cout<< i << ": "<< cnt<< endl; // 디버깅용

        if(cnt == n - 1)
        {
            answer++;
        }
    }
    
    return answer;
}