10장 Collision - ① 기하 타입
게임에서 플레이어가 벽에 부딪히거나 총알이 표적에 맞거나 중력이 작용하는 세계에서 플레이어가 땅을 딛고 서있기 위해서 충돌 검사가 필요하다. 10장에서는 다양한 상황에서 사용할 수 있는 몇 가지 충돌 검사 기법을 다룬다. 그리고 충돌 검사를 위한 기본 기하 타입을 소개한다. 그런 다음 이런 기본 기하 타입 간의 교차 계산을 다룬다. 그리고 게임 메커니즘에 충돌을 포함하는 방법을 설명한다.
💡 10장의 목차
- 기하 타입
- 교차 테스트
- 게임에서 충돌처리
기하 타입
게임에서 충돌 감지를 이해하기 위해서는 몇 가지 기하 타입에 대한 이해가 필요하다. 우리는 아래의 기본 기하 타입에 대해서만 다룬다.
- 선분
- 평면
- 바운딩 볼륨
- 구체
- 축 정렬 바운딩 박스 AABB
- 방향성 있는 바운딩 박스 OBB
- 캡슐
- 볼록 다각형
선분
선분의 정의
선분은 시작 지점과 끝 지점으로 구성되어 있기에 다음과 같이 정의할 수 있다.
struct LineSegment
{
Vector3 mStart;
Vector3 mEnd;
};선분상의 임의의 점을 계산하기 위한 매개 방정식은 다음과 같이 정의할 수 있다.
\[L(t) = Start + (End-Start)t \qquad where\ 0 \le t \le 1\]
이를 함수로 구현하면 다음과 같다.
Vector3 LineSegment::PointOnSegment(float t) const
{
return mStart + (mEnd - mStart) * t;
}선분에서 임의의 점까지 최단 거리
선분에서 자주 사용하게될 연산은 임의의 점과 선분 사이의 최소 거리를 찾는 것이다. 점과 선분 사이의 최소 거리를 찾기 위해서는 아래의 3가지 경우를 살펴볼 필요가 있다.
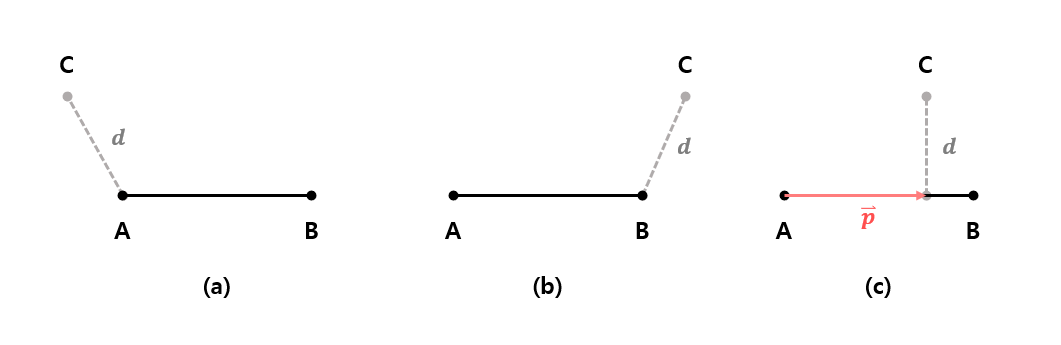
- (a): 선분(벡터) AB와 벡터 AC의 각이 90도 이상일 경우 벡터 AC의 길이가 점과 선분의 최단거리이다.
- (b): 선분(벡터) BA와 벡터 BC의 각이 90도 이상일 경우 벡터 BC의 길이가 점과 선분의 최단거리이다.
- (C): (a)와 (b)에 해당되지 않는 경우 점 C에서 선분 AB로 수선의 발을 내린 선분의 길이가 점과 선분 사이의 최소 거리이다. 이를 구하는 방법은 다음과 같다.
\[d = \lVert \vec{AC} - \vec{p} \rVert\]
d의 길이를 알기 위해서는 \(\vec{p}\)를 알아야 한다. \(\vec{p}\)는 다음과 같다.
\[\vec{p} = \lVert \vec{p} \rVert \frac{\vec{AB}}{\lVert\vec{AB}\rVert}\]
\(\lVert \vec{p} \rVert\) 값은 다음과 같이 구할 수 있다.
\[\lVert \vec{p} \rVert \vec{\lVert AB \rVert} = \vec{AC} \cdot \vec{AB}\]
\[\lVert \vec{p} \rVert = \vec{AC} \cdot \frac{\vec{AB}}{\vec{\lVert AB \rVert}}\]
이 과정을 구현한 코드는 여기에서 LineSegment::MinDistSq함수를 참고하자. 비용이 큰 제곱근 연산을 피하기 위해서 \(d\)가 아니라 \(d^2\)을 계산한다는 것에 유의하자.
평면
평면의 정의
평면은 무한히 확장되는 평평한 2차원 표면이다. 평면의 방정식은 다음과 같다.
\[P \cdot \hat{n} + d = 0\]
\(\hat{n}\)은 평면의 정규화된 법선 벡터이고 \(d\)는 평면과 원점 사이의 부호 있는 최소 거리이다.
평면은 \(\hat{n}\)와 \(d\)만으로 정의되기 때문에 코드로는 다음과 같이 정의할 수 있다.
struct Plane
{
Vector3 mNormal;
float mD;
};평면에서 임의의 점까지 최단 거리
임의의 점 C와 평면 사이의 최소 거리를 구하는 것은 다음과 같다. 이해를 돕기 위해서 아래의 그림은 평면을 측면에서 바라본 모습이다.
- 임의의 점 C를 법선 벡터 \(\hat{n}\)로 투영(내적) 하여 \(s\)를 구한다.
- \(s\)에 \(d\)를 빼면 부호 있는 거리차를 구할 수 있다.
\[SignedDist = s - d = C \cdot \hat{n} - d \]

이를 함수로 구현하면 다음과 같다.
float Plane::SignedDist(const Vector3& point) const
{
return Vector3::Dot(point, mNormal) - mD;
}바운딩 볼륨
3D 게임은 수천 개의 삼각형으로 구성된 캐릭터와 오브젝트로 표현된다. 두 오브젝트의 충돌 여부를 결정하고자 할 때 오브젝트를 구성하는 모든 삼각형의 교차 여부를 테스트하는 것은 효율적이지 못하다. 이런 이유로 게임에서는 박스나 구체 같은 바운딩 볼륨을 사용한다.
구체
그중 구체는 가장 단순화된 경계 표현이다. 구체는 오직 구체의 중심과 반지름 만으로 정의할 수 있다.
struct Sphere
{
Vector3 mCenter;
float mRadius;
};구체는 계산비용이 저렴한 반면 정확도가 떨어진다. 인간을 구체로 표현할 경우 빈 공간이 많이 생기고, 충돌하지 않았지만 충돌했다는 긍정의 오류가 발생할 가능성이 매우 높다.
축 정렬 바운딩 박스 (AABB)
2D에서 AABB 박스는 x축과 y축에 평행한 사각형이다. 3D에서 AABB 박스는 모든 면이 좌표축 평면의 하나와 평행한 사각형 프리즘이다. AABB는 최소점과 최대점 두 점으로 정의한다.
struct AABB
{
Vector3 mMin;
Vector3 mMax;
};AABB 박스를 생성할 때 오브젝트의 모든 정점을 탐색하여 가장 작은 값을 mMin에 가장 큰 값을 mMax에 담는다. 이에 대한 구현은 여기에서 AABB::UpdateMinMax 함수를 참고하자.
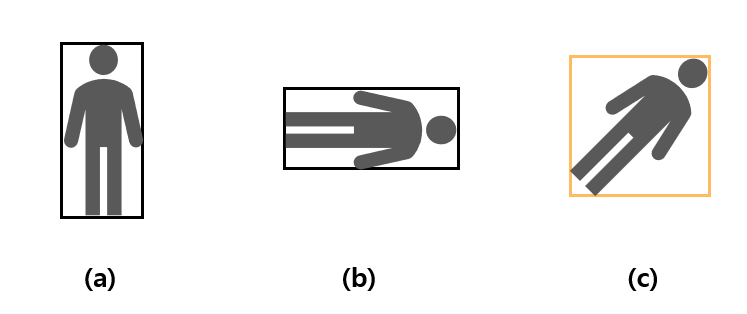
AABB는 항상 축에 평행하도록 구성되기 때문에 회전이 발생할 경우 다시 AABB를 계산해야 하는 등 다소 복잡한 문제가 발생한다.
방향성 있는 바운딩 박스 (OBB)
방향성 있는 바운딩 박스는 AABB처럼 축이나 평면에 대해 평행해야 한다는 제한이 없다. 그래서 회전에 있어서는 AABB 보다 자유롭게 활용할 수 있지만 충돌 계산량이 AABB보다 비싸다는 단점이 있다.

OBB는 다음과 같이 정의한다.
struct OBB
{
Vector3 mCenter;
Quaternion mRotation;
Vector3 mExtents;
};캡슐
캡슐은 반지름을 가진 선분이다.
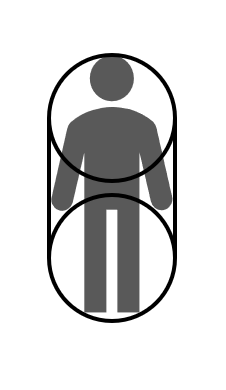
캡슐은 다음과 같이 정의할 수 있다.
struct Capsule
{
LineSegment mSegment;
float mRadius;
};캡슐은 게임에서 인간형 캐릭터를 나타내기 위해 자주 사용된다. 왜냐하면 구체가 이동을 할 때는 시작점과 끝점이 있고, 이동 중의 구체는 반경을 가지고 있기 때문이다.
볼록 다각형
2D 상에서 기본 형태보다 더 정확한 물체의 경계가 필요할 때 볼록 다각형을 사용할 수 있다. 도형 내부 모든 각이 180도보다 작다면 그 다각형은 볼록 다각형이다. 볼록 다각형은 버텍스의 집합으로 정의할 수 있다. 이때 추후 교차 테스트를 위해 버텍스는 반드시 시계 방향으로 정렬되어 있어야 한다.
struct ConvexPolygon
{
// 버텍스는 시계 방향으로 정렬돼 있어야 한다.
std::vector<Vector2> mVertices;
};
출처:
에이콘 출판 <Game Programming in C++>
