[BOJ 8980] 택배 (C++)

택배 Gold 3

문제

전체 문제 보기

8980번: 택배

접근법

이번 문제는 어떻게 접근할지 생각하기 다소 어려운 문제였습니다. 이번 문제 같은 경우 그리디로 풀 수 있지만 DP로 풀어야할지 그리디로 풀어야할지 여러 방향으로 오래 고민을 했습니다. 제가 풀었던 방법은 다음과 같습니다.

 

가장 많은 택배를 배송하기 위해서는 새로운 택배를 많이 받아야 합니다. 새로운 택배를 많이 받기 위해서는 빨리 내릴 수 있는 택배를 먼저 받고 바로 새로운 택배를 받아야 합니다. 즉, 먼저 내리는 택배를 우선적으로 받을 경우 가장 많은 택배를 옮길 수 있게 됩니다. 따라서 택배들을 우선 도착지 기준으로 정렬을 합니다. (아래의 데이터는 문제의 예제 입력 2번 데이터입니다.)

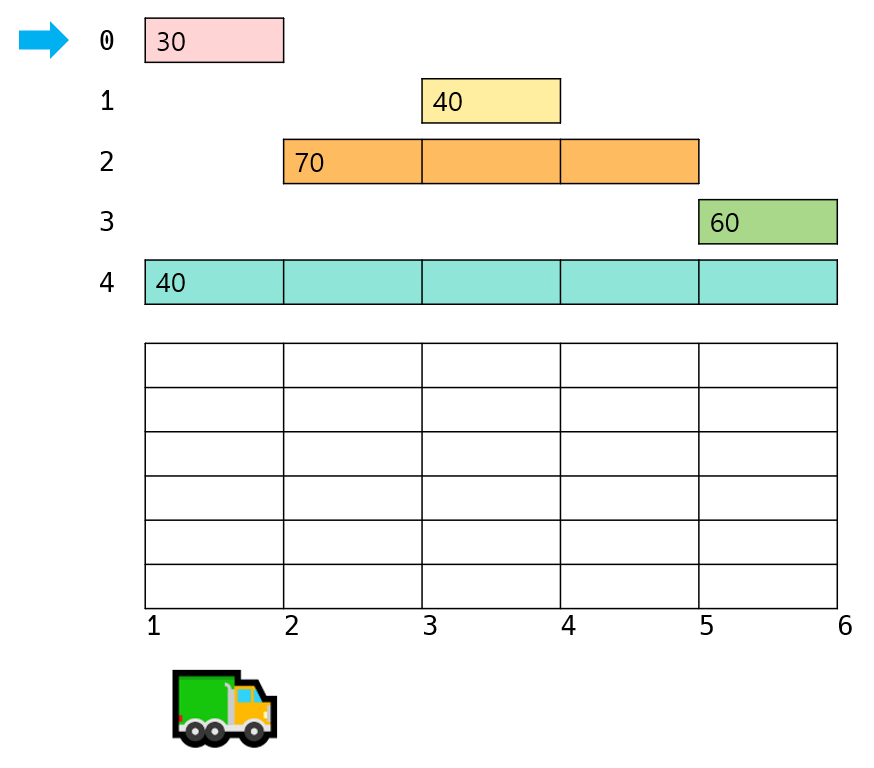
그리고 가장 먼저 2번 마을에서 내릴 택배들을 트럭에 올립니다. 그럼 1~2 구간에서 트럭은 0번 택배(30 상자)를 실을 수 있습니다.

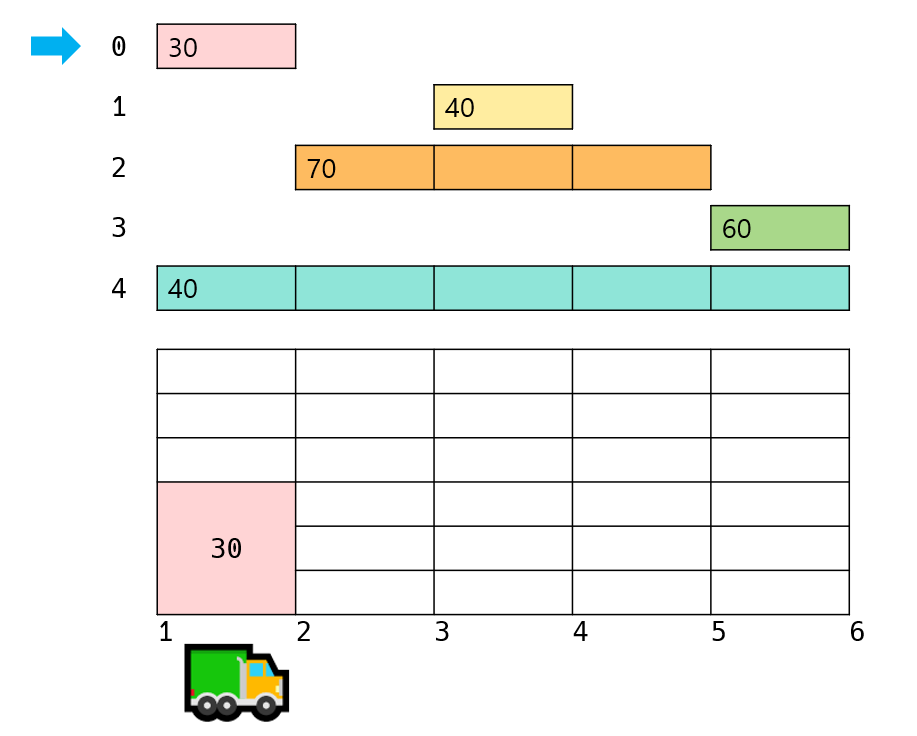
이후 3번 마을에서 내릴 수 있는 택배는 없기 때문에 그냥 지나갑니다. 그리고 4번 마을에서 내려줄 택배를 올립니다. 3~4 구간에 여유가 있기 때문에 1번 택배(40 상자)를 모두 트럭에 올릴 수 있습니다.

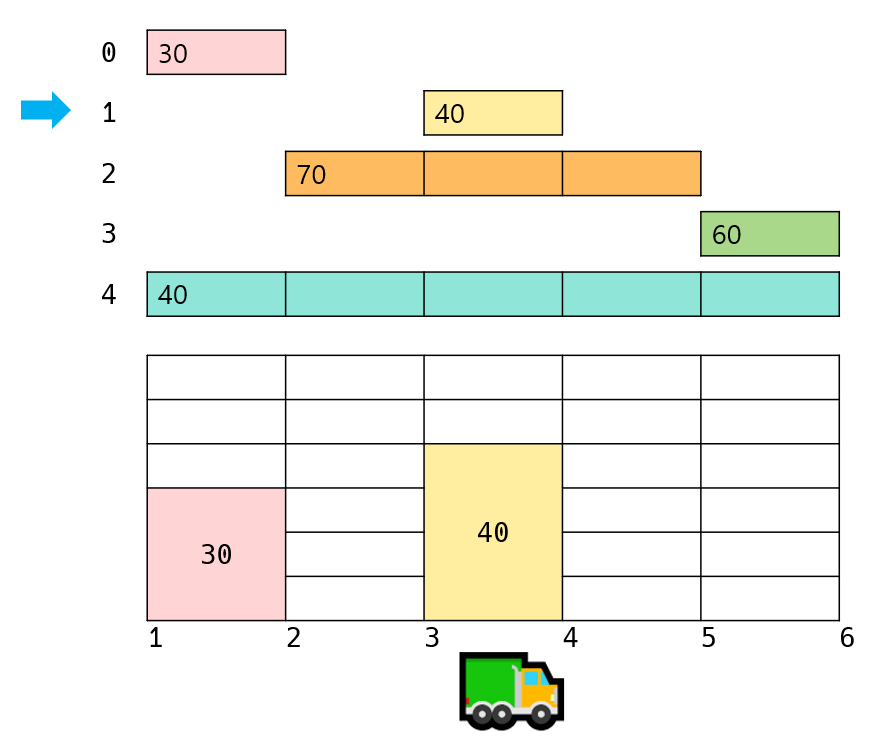
이후 5번 마을에서 내릴 수 있는 택배를 트럭에 실어야 합니다. 그런데 5번 마을에서 내릴 수 있는 3번 택배는 2번 마을에서 출발합니다. 2~5 구간 모두는 최소 20만큼의 공간은 가지고 있습니다. 그래서 20 상자만 트럭에 실을 수 있습니다. 때문에 5번 마을에서는 3번 택배 물량 중 20 상자만 트럭에 올립니다.

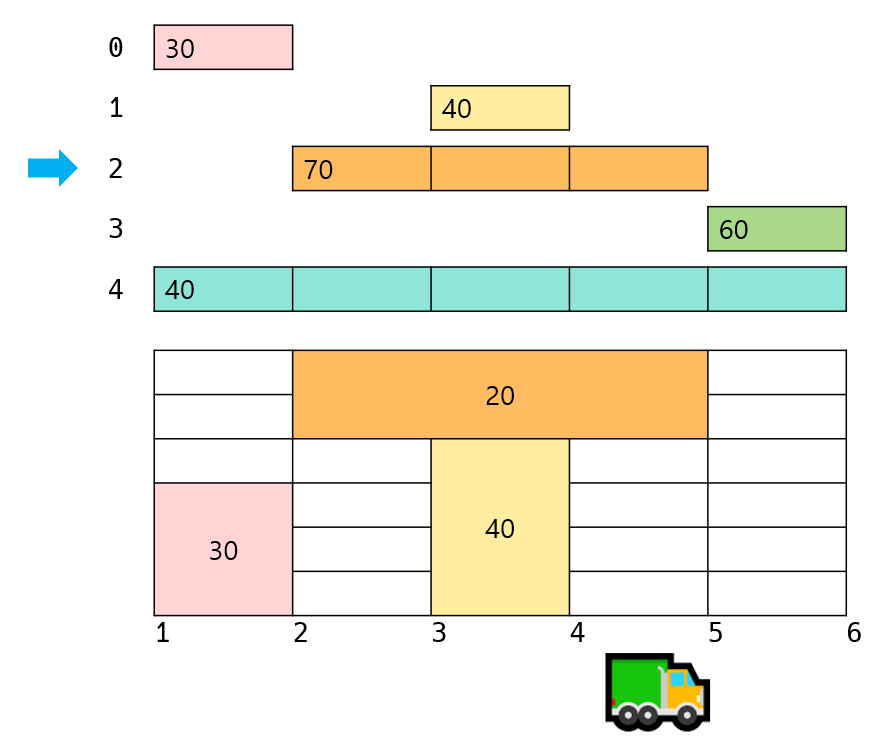
마지막으로 6번 마을에서는 5~6구간에 트럭의 여유가 60만큼 있기 때문에 3번 택배를 모두 실을 수 있습니다. 그리고 4번 택배는 실을 수 있는 공간이 없기 때문에 운반하지 않습니다.

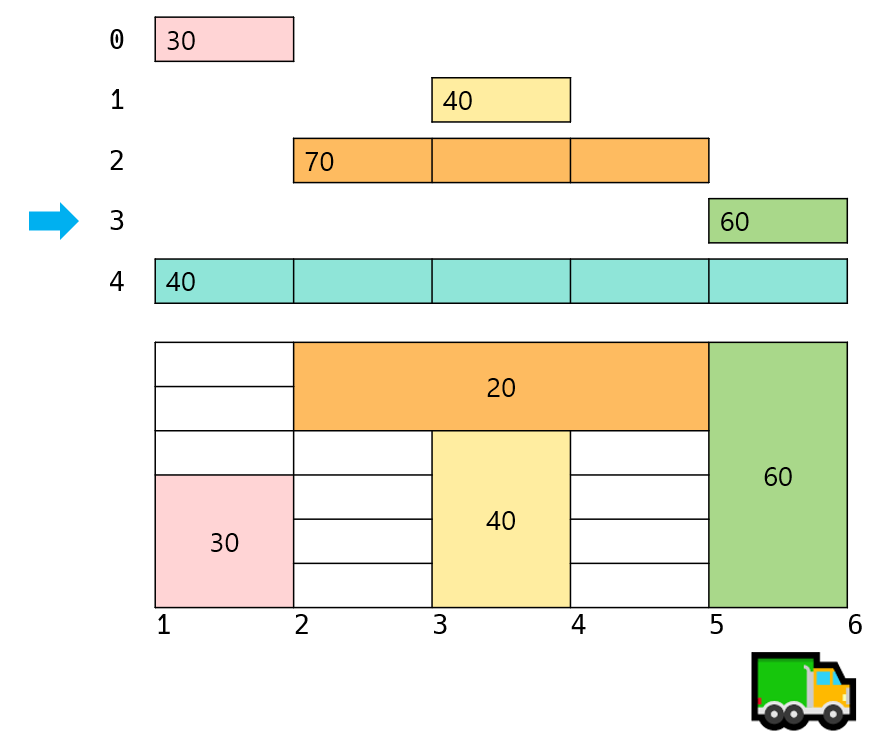
정리하면 다음과 같습니다.

1. 도착지 기준으로 택배를 정렬한다.
2. 각 도착지에서 트럭에 택배를 실을 수 있는 여유가 있는지 확인한다.
3. 트럭에 여유가 있는 만큼 트럭에 상자를 싣는다.
4. 모든 도착지에 대해서 위 작업을 반복한다.

성능 평가

전체적인 시간 복잡도를 평가해보면 다음과 같습니다. 먼저 마을의 개수를 N, 박스의 개수를 M이라고 했을 때 택배를 정렬하기 위해서 \(O(M\mbox{log}M)\)이 걸립니다. 그리고 각 상자마다 택배를 실을 수 있는지 파악하기 위해서 최악의 경우 모든 마을의 개수만큼 탐색해야 합니다. 즉, 택배를 싣기 위해서는 \(O(N \cdot M)\)만큼의 시간이 걸립니다. 그래서 위 알고리즘의 시간 복잡도는 \(O(N \cdot M)\) 입니다.

전체 구현

위 내용을 다음과 같이 구현할 수 있습니다.

#include <iostream>
#include <vector>
#include <algorithm>
#define endl '\n'
using namespace std;
struct Box {
    int from;
    int to;
    int cnt;
    bool operator< (const Box& other) { return to < other.to; }
};
constexpr int INF = 987'654'321;
int main()
{
    //입출력 성능향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);

    int N, C; // 마을 수 N, 트럭의 용량 C / N은 2이상 2,000이하 정수, C는 1이상 10,000이하 정수
    cin >> N >> C;
    int M; // 보내는 박스 개수(1이상 10,000이하 정수)
    cin >> M;
    vector<Box> boxes(M);
    for (int i = 0; i < M; ++i)
    {
        cin >> boxes[i].from >> boxes[i].to >> boxes[i].cnt;
    }
    sort(boxes.begin(), boxes.end());

    // i 위치에서 트럭의 빈공간(C로 초기화)
    vector<int> truck(N+1,C); 

    int idx{}; // box index
    int shippedBox{};
    for (int i = 1; i < N+1; ++i)
    {
        // 현재 집이 첫번째 박스의 목적지 앞에 있다면 continue
        if (boxes[idx].to > i) continue;

        while (idx < M && boxes[idx].to == i)
        {
            // 잔여공간
            int space{ INF };
            for (int j = boxes[idx].from; j < boxes[idx].to; ++j)
            {
                space = min(truck[j], space);
            }
            if (space >= boxes[idx].cnt) // 잔여 공간이 넉넉하다면
            {
                shippedBox += boxes[idx].cnt; // 배송된 상자 수에 현재 배송물량 모두 추가
                for (int j = boxes[idx].from; j < boxes[idx].to; ++j) // 각 위치 트럭의 빈공간 감소
                {
                    truck[j] -= boxes[idx].cnt;
                }
            }
            else if (space > 0) // 잔여공간이 조금 남았다면
            {
                shippedBox += space;
                for (int j = boxes[idx].from; j < boxes[idx].to; ++j)
                {
                    truck[j] -= space;
                }
            }
            idx++;
        }
    }

    //for (int i = 0; i < N+1; ++i)
    //{
    //    cout << C - truck[i] << " ";
    //}
    cout << shippedBox << endl;
    return 0;
}