[BOJ 2229] 조 짜기 (C++)

조 짜기 (Gold 5)

문제

전체 문제 보기

2229번: 조 짜기

접근법

이번 문제는 동적 계획법을 활용하여 \(O(n)\) 시간 복잡도로 풀 수 있는 문제입니다. 동적 계획 법으로 문제를 풀기 위해서는 일반화하는 과정이 필요합니다.
먼저 동적 계획법에서 사용할 dp[i]은 i번째 사람까지 조를 짰을 경우 최댓값으로 정의할 수 있습니다. 그리고 초기값은 다음과 같이 설정할 수 있습니다.

dp[0]은 0번 사람 한 명만 들어오기 때문에 최대 값은 0일 수밖에 없습니다.
dp[1]은 두 명뿐이기 때문에 조를 짤 수 있는 경우는 2, 5 뿐이기 때문에 3이 됩니다.

2번 사람이 새로 들어올 경우에는

• 2번 사람이 기존의 조에 합류하는 방법
• 1번 사람과 2번 사람이 새로 조를 꾸리는 방법
  이 있습니다. 이중 최댓값이 dp[2]가 될 수 있습니다. 여기서는 기존의 조에 합류하는 방법이 더 효율적이기 때문에 dp[2]는 5가 됩니다.

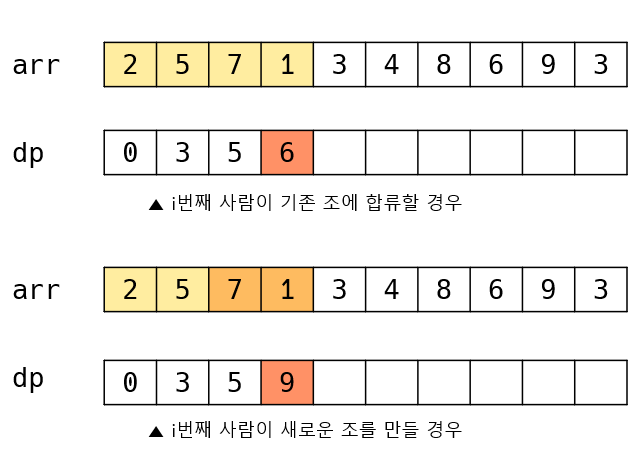
3번 사람이 새로 들어올 경우에는

• 3번 사람이 기존의 조에 합류하는 방법
• 2번 사람과 3번 사람이 새로 조를 꾸리는 방법
  이 있습니다. 여기에서는 조를 새로 꾸리는 방법이 더 효율적이기 때문에 dp[3]은 9가 됩니다.

이렇게 바텀업 방식으로 n번째 까지 계산하면 \(O(n)\) 시간 복잡도로 답을 구할 수 있습니다.

전체 코드

#include <iostream>
#include <vector>
#include <cmath>
#include <algorithm>
#define endl '\n'
using namespace std;

int main()
{
    //입출력 성능향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);

    int N; //  N(1≤N≤1,000)
    cin >> N;
    vector<int>arr(N);
    vector<int>dp(N);
    for (int& n : arr)
    {
        cin >> n;
    }

    dp[0] = 0;
    dp[1] = abs(arr[0] - arr[1]);
    int minval = min(arr[0], arr[1]);
    int maxval = max(arr[0], arr[1]);

    for (int i = 2; i < N; ++i)
    {
        int a = dp[i - 1];
        if (maxval < arr[i])
        {
            a += (arr[i] - maxval);
        }
        else if (minval > arr[i])
        {
            a += (minval - arr[i]);
        }
        int b = dp[i - 2] + abs(arr[i - 1] - arr[i]);

        if (a > b)
        {
            dp[i] = a;
            if (maxval < arr[i])
            {
                maxval = arr[i];
            }
            else if (minval > arr[i])
            {
                minval = arr[i];
            }
        }
        else
        {
            dp[i] = b;
            minval = min(arr[i - 1], arr[i]);
            maxval = max(arr[i - 1], arr[i]);
        }
    }
    cout << dp[N - 1] << endl;
    return 0;
}

실행 결과