4장 인공지능 - ③ 게임트리와 AI의 의사결정 내리기
인공지능(AI, Artificial Intelligence)알고리즘은 게임에서 컴퓨터가 제어하는 오브젝트의 행위를 결정하는 데 사용한다. 4장에서는 3가지의 유용한 AI 게임 테크닉을 다룬다.
💡 4장의 목차
- 상태 기계로 행위 변경하기
- 오브젝트가 세계 주변을 돌아다니도록 경로 계산하기(길 찾기)
- 2인용 턴 기반 게임(미니맥스와 게임 트리)에서 의사결정 내리기
- 게임 트리
- 미니 맥스
- 불완전 게임 트리 다루기
게임 트리
게임 트리란 체스, 장기, 바둑, 틱택토 등 2명의 플레이어가 차례를 번갈아가며 진행하는 게임에서 발생할 수 있는 모든 경우를 트리로 표현한 것을 말한다. 게임 트리의 노드는 말들의 위치를 표현한 하나의 상황을 나타낸다. AI가 다음 수를 결정할 때 이 게임트리를 활용하여 가장 최적의 수를 결정 할 수 있다.
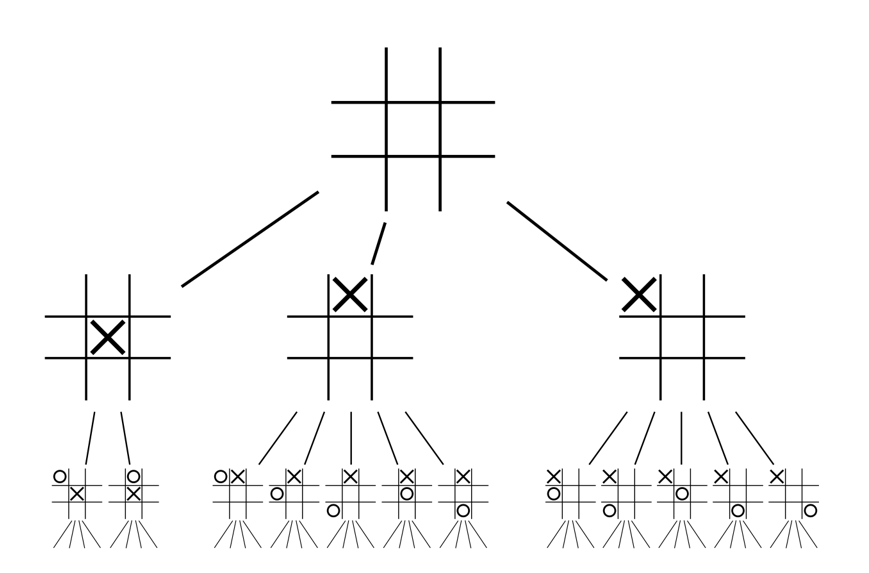
여러 게임들은 다양한 상태를 가질 수 있고 틱택토같 이 모든 상태를 노드로 갖는 게임 트리를 완전한 게임 트리라고 한다. 틱택토는 3 x 3 맵에서 진행되는 단순한 게임으로 발생 가능한 모든 경우의 수는 9!, 즉 362,880개의 경우의 수가 존재한다. 틱택토를 완전한 게임 트리로 다루기 위해서는 362,880개의 노드가 필요하다. 하지만 체스의 경우 완전한 게임 트리는 \(10^{120}!\)의 노드가 필요하므로 시간과 공간의 복잡도를 완전히 평가하는것이 불가능 하다.
틱택토와 같은 배열 형식의 보드게임의 게임트리의 노드는 다음과 같이 정의할 수 있다.
틱택토 게임 상태와 노드
struct GameState
{
enum SquareState {empty, X, O};
SquareState mBoard[3][3];
}
struct GTNode
{
// 자식 노드
std::vector<GTNode*> mChildren;
// 이 노드의 게임 상태
GameState mState;
}
미니맥스
미니맥스는 손실을 최소화 한다는 뜻이 있다. 그래서 미니맥스 알고리즘은 2인용 게임 트리를 평가해서 자신의 점수 손실을 최소화 할수 있는 이동을 결정한다.
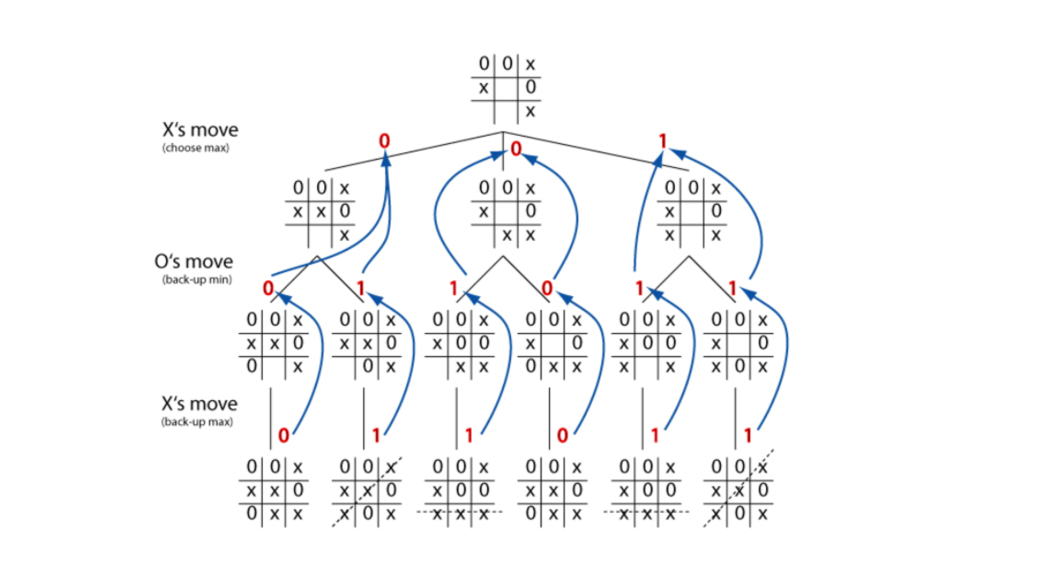
x를 맥스 플레이어, o를 민 플레이어라고 했을 때 각각의 플레이어의 다음 수를 결정 하는 함수는 다음과 같다.
- 두 함수 모두 최초에는 노드가 리프 노드인지를 시험한다.
- 리프 노드일 경우
GetScore()함수를 호출해서 점수를 계산한다. - 두 함수는 재귀 호출을 사용해서 최선의 하위 트리를 결정한다.
- 맥스 플레이어는 가장 높은 값을 산출하고 민 플레이어는 가장 낮은 값을 산출한다.
- 산출된 값을 바탕으로 다음 수를 결정한다.
미니맥스 구현
미니맥스를 구현하기 위해서 3가지의 함수가 정의되었다.
MaxPlayer(): 현재 노드에서 가장 높은 값을 산출하는 함수. 점수에 해당하는float값 반환MinPlayer(): 현재 노드에서 가장 낮은 값을 산출하는 함수. 점수에 해당하는float값 반환MinmaxDecide(): 어떤 자식 노드가 최선의 값을 산출하는지 추적하는 함수. 즉 다음수를 결정하는 함수이다. 다음 수에 해당하는GTNode*반환
전체 소스코드
불완전 게임 트리 다루기
앞서 언급했듯이 항상 완전 게임 트리를 생성하는 것은 시간, 공간상으로 불가능 하다. 때문에 사전에 트리를 생성하기보다는 실행 시간 동안에 트리를 생성하는 불완전 게임 트리를 다루는 방법이 필요하다.
이 불완전 게임 트리에 대한 접근법은 사람이 체스를 두는 것과 비슷한 방식이다. 일반적인 체스 플레이어는 게임의 끝까지 모든 경우의 수를 예측할 수 없다. 단지 몇 수 앞을 내다 볼 뿐이다. 이처럼 AI도 게임 트리의 깊이를 제한해야 한다. 즉, 코드는 노드가 게임 상태의 마지막에 있지 않다 하더라도 그 노도를 리프노드로 다룬다는 것을 뜻한다.
이를 위해서는 종료되지 않은 상태를 종료된 것과 비슷하게 근사화하는 휴리스틱 요소가 필요하다. 휴리스틱 요소를 사용하게 되면 미니맥스 처럼 최적의 결정이 아니라 차선의 결정이고 미니맥스에 비교하면 손실이 발생할 수밖에 없다. 하지만 미니맥스를 구현하기 위해 완전 게임 트리를 만드는 것은 불가능 한 일이지만 휴리스틱을 활용해서 불완전 게임 트리를 다루는 일은 가능한 일이다.
불완전 게임 트리 구현
불완전 게임 트리를 구현하기 위해서는 미니맥스를 일부 수정해야한다. 아래는 불완전 게임트리를 위한 함수 일부분이다. 이 코드에는 GameState가 3개의 멤버 함수 IsTerminal,GetScore,GetPosiibleMove를 가지고 있다고 가정한다.
IstTerminal(): 상태가 종료되면true반환GetScore(): 함수는 종료되지 않은 상태의 휴리스틱 값을 리턴하거나 종료 상태의 점수를 반환GetPossibleMove(): 현재 상태 이후에 움직일 수 있는 이동에 대한 게임 상태 벡터 리턴
float MaxPlayerLimit(const GameState* state, int depth)
{
// depth가 0이거나 상태가 terminal이면 최대 깊이에 도달했다는 걸 뜻한다.
if(depth == 0 || state->IsTerminal())
{
return state->GetScore();
}
// 최댓값을 가진 하위 트리를 찾는다.
float maxValue = -std::numeric_limits<float>::infinity();
for(const GameState* child : state->GetPossibleMoves())
{
maxValue = std::max(maxValue, MinPlayer(child, depth - 1));
}
return maxValue;
}AI 플레이어의 성능에 직접적인 영향을 미치는 부분은 휴리스틱 함수와 연산의 깊이일 것이다. 휴리스틱 함수는 게임에 따라 다양하게 존재할 수 있다. 예를 들어 체스 게임의 휴리스틱 함수는 각 플레이어가 가진 말의 수를 세고 각각의 말에 가중치를 부여하는 것일 수 있다. 하지만 이러한 휴리스틱 함수로는 짧은 기간에 말을 희생해서 더큰 이득을 얻는 전략은 취할 수 없다.
불완전 트리에서 연산량은 탐색하고자 하는 깊의의 지수만큼 증가하게 된다. 더 많은 수를 예측하기 위해서는 굉장히 많은 시간이 필요하다. 때문에 AI에 시간제한을 하게 되면 AI 성능에 많은 영향을 미치게 된다.
본 게시글은 에이콘 출판사의 Game Programming in C++ 도서를 학습하며 요약 정리한 내용입니다.
