[BOJ 11066] 파일 합치기(C++)

파일 합치기(Gold3)

문제

전체 문제 보기

11066번: 파일 합치기

접근법

이번 문제는 동적 계획법으로 풀 수 있는 문제입니다. 동적 계획법의 주요한 두 가지 개념은 다음과 같습니다.

1. 큰 문제를 작은 문제로 나눠서 문제를 해결한다.
2. 한번 푼 문제를 저장하여 불필요한 연산을 줄인다.

우선 큰 문제를 작은 문제로 나눠 봅시다. 문제의 첫 번째 예시 (40 30 30 50) 인경우를 살펴보겠습니다. 장의 수가 총 4개일 때 마지막으로 파일을 합쳐서 하나로 만들 때는 다음과 같이 3가지의 경우가 존재할 것입니다.

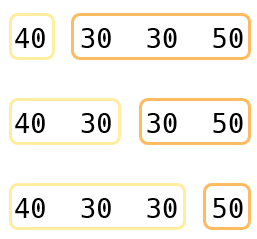
위의 그림 에서 장의 수가 3개인 묶음은 아래와 같이 다시 나눠질 수 있습니다.

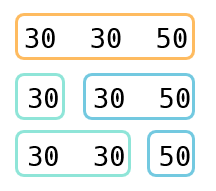
장의 수가 1개인 경우는 묶음을 위해서 비용이 발생하지 않기 때문에 더 이상 나눌 수 없습니다. 결국 정리하면 장의 수가 4개인 경우에는 (1 + 3) / (2 + 2) / (3 + 1)로 나눌 수 있고, 장의 수가 3개인 경우 (1 + 2) / (2 + 1)로 문제를 나눌 수 있습니다. 그래서 장의 수가 4개인 경우에는 3가지 경우에 대해서만 비교를 해도 전체 경우의 수를 비교한 것과 같은 값을 얻을 수 있습니다.

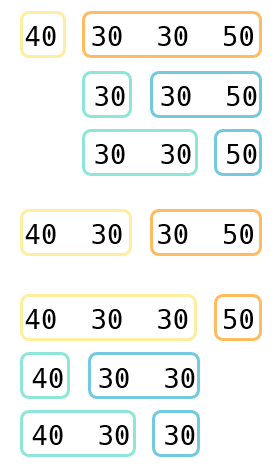
동적 계획법의 가장 핵심은 한번 푼 문제를 저장하여 중복된 연산을 줄인다는 점입니다. 이를 위해서 다음과 같이 배열을 정의하여 중복된 계산을 줄여줄 수 있습니다.

// dp[pos][size] : pos 위치에서 size 개수로 묶은 경우 최솟값
vector<vector<int>> dp;

전체 구현

#include <iostream>
#include <vector>
#include <algorithm>
#define endl '\n'
using namespace std;
constexpr int INF = 987'654'321;
vector<int> arr;
// dp[pos][size] : pos 위치에서 size 개수로 묶은 경우 최솟값
vector<vector<int>> dp;
int N;

void solve()
{
    cin >> N;

    arr.resize(N + 1,0);
    dp.resize(N + 1);
    for (int i = 1; i < N + 1; ++i)
    {
        cin >> arr[i];
        arr[i] += arr[i - 1];
    }

    for (int i = 1; i < N + 1; ++i)
    {
        dp[i].resize(N + 1, INF);
    }
    // 초기값 설정
    for (int pos = 1; pos < N + 1; ++pos)
    {
        dp[pos][1] = 0;
    }

    for (int size = 2; size < N; ++size)
    {
        for (int pos = 1; (pos + size - 1) < N + 1; ++pos)
        {
            for (int k = 1; k < size; ++k)
            {
                dp[pos][size] = min(dp[pos][size], dp[pos][k] + dp[pos + k][size - k]);
            }
            dp[pos][size] += arr[pos + size - 1] - arr[pos - 1];
        }
    }

    for (int k = 1; k < N; ++k)
    {
        dp[1][N] = min(dp[1][N], dp[1][k] + dp[1 + k][N - k]);
    }
    dp[1][N] += arr[1 + N - 1];

    cout << dp[1][N] << endl;

    arr.clear();
    dp.clear();
}
int main()
{
    //입출력 성능향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);

    int T;
    cin >> T;
    while (T--)
    {
        solve();
    }

    return 0;
}

성능 평가

이 알고리즘에서 가장 큰 시간 복잡도를 가지는 곳은 3중 for문입니다. 각 분기는 장의 개수인 N에 선형적으로 비례하고 있습니다. 따라서 전체 시간 복잡도는 \(O(N^3)\) 입니다. 공간 복잡도는 한번 연산한 결과를 캐싱하기 위해서 사용되는 dp 배열의 크기에 의존하고 있습니다. dp의 크기는 \(N^2\)에 비례하므로 전체 공간 복잡도는 \(O(N^2)\)입니다.