[BOJ 15649] N과 M (1) (C++)

N과 M(1) (Silver 3)

문제

전체 문제 보기

15649번: N과 M (1)

접근법

이 문제는 1 ~ N까지의 자연수 M개를 조합하여서 나올 수 있는 모든 수열을 만드는 문제로 백트래킹으로 풀 수 있는 문제입니다. 백트레킹은 모든 조합을 시도해서 문제의 해를 찾는 알고리즘입니다. 백트레킹의 가장 큰 장점은 불필요한 자식 노드(경우의 수 및 조합) 탐색을 배제함으로 계산시간을 단축할 수 있다는 점입니다. 백트레킹은 재귀적으로 구현할 수 있습니다. 재귀적으로 구현하기 때문에 코드는 간결하지만 직관적으로 이해하기는 어렵습니다. 우선 백트레킹 구현 코드 일부를 보고 아래의 그림을 통해 설명하겠습니다. 아래의 그림은 N이 3이고 M이 2인 경우입니다.

vector<vector<int>>  answer;
bool IsContain[9];
int N, M; // (1 ≤ M ≤ N ≤ 8)

void Backtracking(vector<int>& comb, int depth)
{
    if (depth == M)
    {
        answer.push_back(comb);
        return;
    }

    for (int i = 1; i <= N; ++i)
    {
        if (IsContain[i] == true) continue;

        comb.push_back(i);
        IsContain[i] = true;

        Backtracking(comb, depth + 1);
        comb.pop_back();
        IsContain[i] = false;
    }
}
int main()
{
    cin >> N >> M;
    // 수들의 조합 배열
    vector<int> comb;
    Backtracking(comb, 0);
    for (auto& row : answer)
    {
        for (int num : row)
        {
            cout << num << " ";
        }
        cout << endl;
    }

    return 0;
}

우선 main 함수에서 수들의 조합(Combination)을 만들 comb 배열을 만듭니다. 처음 comb 배열은 비어있습니다. 앞으로 이 comb 배열에 수들을 추가해서 원하는 조합들을 만들어 나갈 예정입니다. 이 comb 배열을 Backtracking 함수에 전달합니다. 두 번째 인자는 재귀 호출의 깊이 값입니다. 처음 호출하기 때문에 0을 전달합니다. Backtracking의 첫 번째 조건문에서 깊이 값이 아직 0이기 때문에 첫 번째 조건문은 지납니다. 이제 중요한 (IsContain[i] == true) ? 조건을 만납니다. comb 배열에 i라는 숫자가 있는지 확인하는 과정입니다. 아직 comb 배열은 비어있기 때문에 무사히 통과할 수 있습니다. 이 과정을 그림으로 표현하면 다음과 같습니다.

조건문을 무사히 통과한 않다면 isContain[1]을 true로 설정하고 1을 삽입합니다. 그리고 1이 삽입된 comb 배열을 다시 깊이가 1인 백트래킹 함수로 호출합니다. 깊이가 1인 백트래킹 함수에서도 for문에서 1이 포함되어있는지 묻습니다.

 

그런데 이미 배열에는 1이 포함되어 있기 백트래킹 함수를 다시 호출하지는 않습니다.

다음으로 comb 배열에 2가 포함되었는지 묻습니다. 2가 포함되지 않았기 때문에 comb에 2를 추가한 후 깊이 값을 1 증가시킨 백트래킹 함수를 호출합니다.

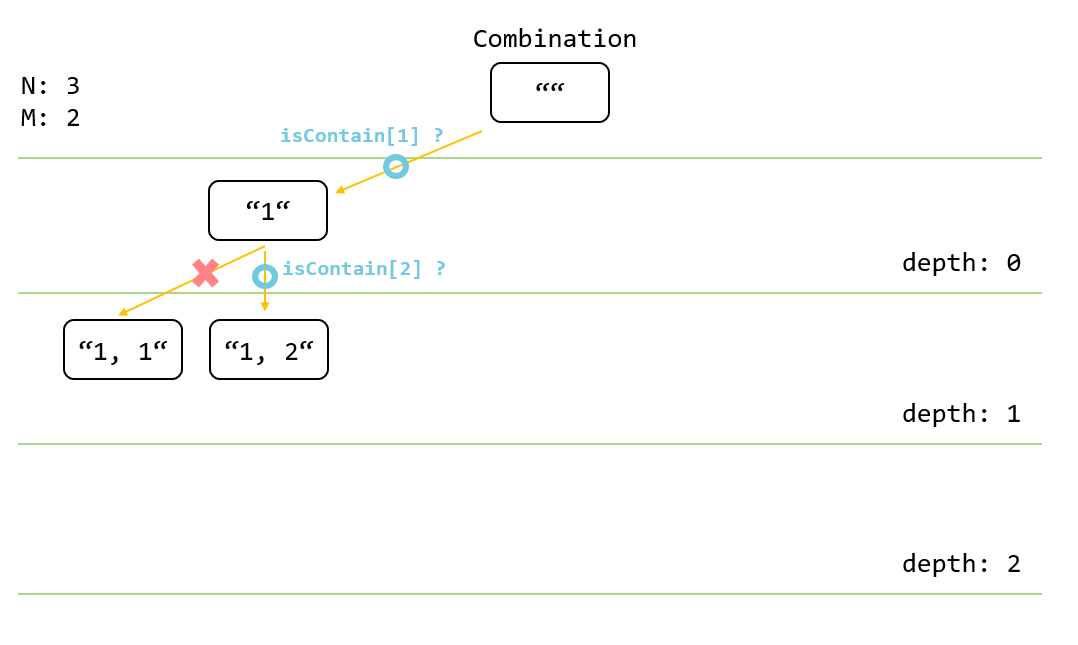
이번에는 깊이가 2인 백트래킹 함수가 호출되었습니다. 깊이 값이 M과 같아졌습니다. 그럼 이제 answer 배열에 현재 comb 수열을 추가한 현재 깊이의 백트래킹 함수를 반환합니다.

다시 깊이 1수준의 백트래킹 함수의 for문으로 돌아왔습니다. 다시 백트래킹 코드의 for문을 살펴봅시다.

    for (int i = 1; i <= N; ++i)
    {
        if (IsContain[i] == true) continue;

        comb.push_back(i);
        IsContain[i] = true;

        Backtracking(comb, depth + 1);
        comb.pop_back();
        IsContain[i] = false;
    }

백트래킹 함수가 종료되면 comb 배열에서 마지막 수를 pop합니다. comb 배열은 {1, 2} 에서 다시{ 1 }이 되었습니다. 이제 i가 3인경우를 살펴봅니다. comb 배열에 3이 포함되어있는지 묻습니다. comb 배열에는 3이 없기 때문에 아래의 코드들이 실행됩니다. 3인 경우도 2의 경우와 마찬가지로 깊이가 2인 백트래킹 함수를 호출합니다.

깊이가 2인 백트래킹 함수가 호출되었기 때문에 answer 배열에 현재 comb 배열을 추가한 후 바로 반환하였습니다. 이제 깊이가 1인 백트래킹 함수의 반복문이 모두 끝났습니다. 그래서 깊이가 1인 백트래킹 함수를 반환하고 깊이가 0인 백트래킹 함수로 넘어 갑니다. 깊이가 0인 백트래킹 함수에서도 마찬가지로 2와 3에 대해서 계속 동일하게 탐색을 진행하여 답을 구할 수 있습니다.

이상으로 백트래킹 알고리즘 구현에 대한 설명을 마칩니다.

전체 구현

백트래킹 알고리즘에서 배열을 주고받을 때 주소 값을 전달하는지, 값을 전달하는지 주의하며 코드를 작성해야 합니다.

#include <iostream>
#include <vector>
#define endl '\n'
using namespace std;

vector<vector<int>>  answer;
bool IsContain[9];
int N, M; // (1 ≤ M ≤ N ≤ 8)

void Backtracking(vector<int>& comb, int depth)
{
    if (depth == M)
    {
        answer.push_back(comb);
        return;
    }

    for (int i = 1; i <= N; ++i)
    {
        if (IsContain[i] == true) continue;

        comb.push_back(i);
        IsContain[i] = true;

        Backtracking(comb, depth + 1);
        comb.pop_back();
        IsContain[i] = false;
    }
}
int main()
{
    //입출력 성능향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);
    cin >> N >> M;
    // 수들의 조합 배열
    vector<int> comb;
    Backtracking(comb, 0);
    for (auto& row : answer)
    {
        for (int num : row)
        {
            cout << num << " ";
        }
        cout << endl;
    }

    return 0;
}