[BOJ 1504] (Dijkstra)특정 최단 경로(C++)

특정 최단 경로(Gold 4)

문제

전체 문제 보기

1504번: 특정한 최단 경로

접근법

이 문제는 양의 가중치를 간선을 가진 그래프에서 최단 경로를 찾는 문제의 변형이다. 출발 노드 1에서 도착 노드 N까지 가는 도중 v1과 v2 노드를 반드시 지나야 한다. 그리고 아래의 그림처럼 1 → v1 → v2 → N으로 가는 경로와 1 → v2 → v1 → N 으로 가는 경로 두 가지가 존재하고 이 둘 중 더 가까운 경로의 거리를 출력해야 한다.

▲1  →  v1  →  v2  →  N (v1: 5 / v2: 8)

▲ 1  →  v2  →  v1  →  N (v1: 5 / v2: 8)

 

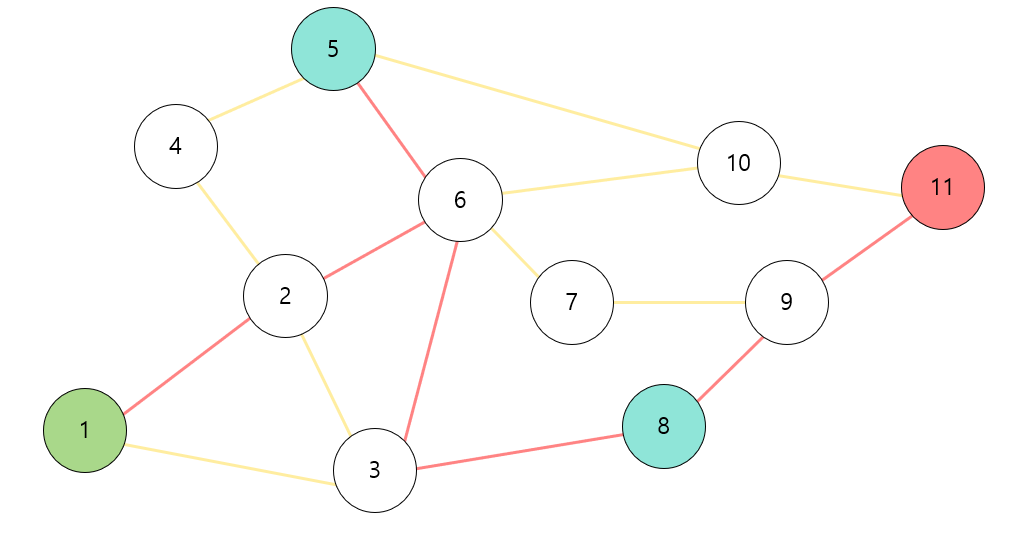
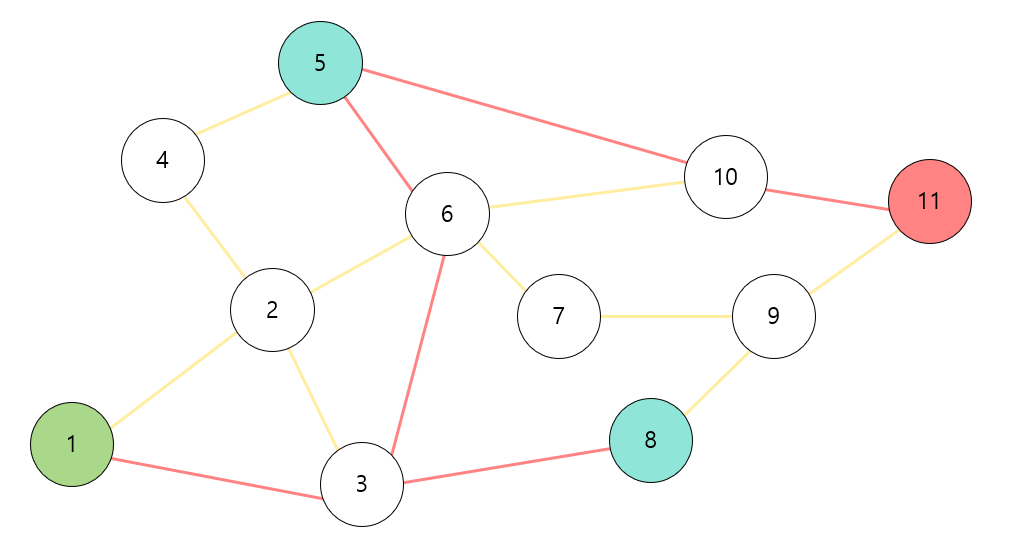
알고리즘 선택

우리가 필요한 최단거리는 다음과 같다.

• 1 → v1 / 1 → v2
• v1 → v2 / v1 → N
• v2 → v1 / v2 → N

가중치의 간선을 가진 그래프에서 최단 경로를 찾는 방법으로 다익스트라 알고리즘과 플로이드 워셜 알고리즘이 존재한다.

• 다익스트라: 한 정점에서 모든 경로로의 최단경로를 계산 / 시간 복잡도 \(O((E + n)\mbox{log}n)\)
• 플로이드 워샬: 모든 정점들 간의 최단 경로 계산 / 시간 복잡도 \(O(n^3)\)

우리가 구해야 하는 경로는 1에서 출발한 최단거리, v1에서 출발하는 최단거리, v2에서 출발하는 최단거리를 반복해서 구해야 하긴 하지만, 이를 위해서 플로이드 워샬을 사용하기에는 너무 느리다. 문제에서 정점의 개수는 800로 주어졌기 때문에 플로이드 워샬 알고리즘을 사용할 경우 약 5억 회 연산이 필요하다. 따라서 다익스트라를 3번 쓰는 방법이 더 합리적이다.

전체 구현

#include <iostream>
#include <queue>
#include <vector>
#include <array>

#define endl '\n'
using namespace std;
// 타입 지정
struct Edge {
    Edge(int _to, int _w) : to(_to), w(_w) {}
    int to;
    int w;
};

struct Path {
    Path(int _v, int _d) : v{ _v }, d{ _d } {}
    int v;
    int d;
};
struct Compare {
    bool operator()(const Path& lhs, const Path& rhs)
    {
        return lhs.d > rhs.d;
    }
};
// 전역변수
int N, E, v1, v2;
const int INF{ 87'654'321 };
vector<vector<Edge>> edges;
vector<int> dist;

void Dijkstra(int s)
{
    // 거리 값 초기화
    for (int i = 1; i < N + 1 ; ++i)
    {
        dist[i] = INF;
    }
    priority_queue<Path, vector<Path>, Compare> q;

    dist[s] = 0;
    q.push({ s, 0 });
    
    while (!q.empty())
    {
        Path cur = q.top();
        q.pop();
        
        for (const Edge& edge : edges[cur.v])
        {
            Path newPath(edge.to, cur.d + edge.w);
            if (newPath.d < dist[newPath.v])
            {
                q.push(newPath);
                dist[newPath.v] = newPath.d;
            }
        }
    }
}
int main()
{
    //입출력 성능향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);


    cin >> N >> E;

    // node 노드 N+1 개 생성
    edges.resize(N + 1);
    dist.resize(N + 1);

    // 모든 간선 연결
    for (int i = 0; i < E; ++i)
    {
        int a, b, weight;

        cin >> a >> b >> weight;
        edges[a].emplace_back(b, weight);
        edges[b].emplace_back(a, weight);

    }

    cin >> v1 >> v2;
    array<array<int, 4>, 4> atob{};

    // 1번 노드를 기준으로 최단 경로 계산
    Dijkstra(1);
    atob[0][1] = dist[v1];
    atob[0][2] = dist[v2];

    // v1번 노드를 기준으로 최단 경로 계산
    Dijkstra(v1);
    atob[1][2] = dist[v2];
    atob[1][3] = dist[N];

    // v2번 노드를 기준으로 최단 경로 계산
    Dijkstra(v2);
    atob[2][1] = dist[v1];
    atob[2][3] = dist[N];

    int answer{};
    const int first = atob[0][1] + atob[1][2] + atob[2][3];
    const int second = atob[0][2] + atob[2][1] + atob[1][3];

    answer = min(first, second);
    if (answer >= INF) answer = -1;
    cout << answer;

    return 0;
}

성능 평가

이 풀이에서는 다익스트라 알고리즘을 3번 반복해서 사용했다. 다익스트라 알고리즘의 반복문을 살펴보자. 첫 번째 while문은 모든 최대 모든 정점의 개수만큼 시행된다. 그런데 q에 삽입 삭제를 하기 위해서는 \(\mbox{log}n\)만큼의 시간이 필요하다. 그리고 while문 안의 for문을 살펴보자. for문은 전체 간선의 수만큼 수행됨을 알 수 있다. 그리고 각 for문의 분기에서는 q에 삽입하기 때문에  \(\mbox{log}n\)의 시간이 걸린다. 따라서 전체 시간 복잡도는 \(O((E + n)\mbox{log}n)\) 임을 계산할 수 있다. 공간 복잡도는 우선 모든 노드의 개수를 저장할 배열과, 노드 구조체 내부에서 모든 간선을 저장하기 위한 배열이 사용됨을 알 수 있다. 따라서 공간 복잡도는 \(O(E + N)\)임을 알 수 있다.