[BOJ 11053] 가장 긴 증가하는 부분 수열 (C++)

가장 긴 증가하는 부분 수열 (Silver 2)

문제

전체 문제 보기

11053번: 가장 긴 증가하는 부분 수열

접근법

가장 긴 증가하는 부분 수열 (Longest Increasing Subsequence) 문제는 동적 프로그래밍 문제 중에서 유명한 문제 중 하나이다. 두 가지의 풀이 방법이 존재하는데 상대적으로 이해하기 쉬운(상대 적으로 쉬운 것이지 결코 쉽지만은 않다.) \(O(N^2)\) 시간 복잡도를 가진 풀이와 직관적으로 바로 이해하기는 조금 어렵지만 시간 복잡도가 \(O(n\mbox{log}n)\)인 풀이가 있다. 먼저 시간 복잡도가 \(O(N^2)\) 인 풀이를 살펴보자. 먼저 아래와 같이 수열 {3, 5, 1, 6, 5, 7, 4}가 존재한다고 하자.

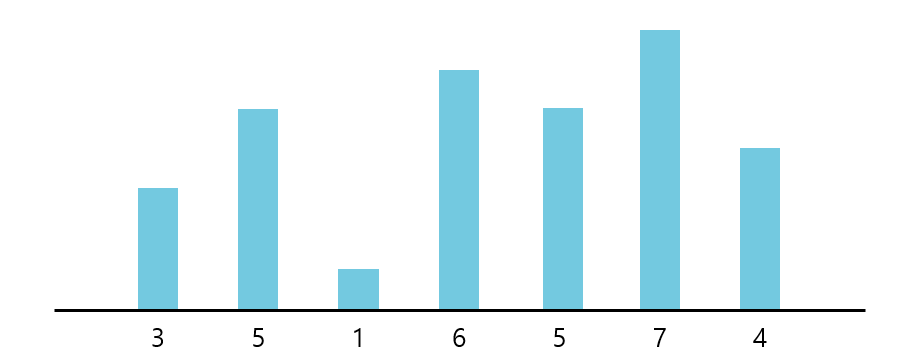
수열 {3, 5, 1, 6, 5, 7, 4}에서 각 숫자로 끝나는 가장 긴 증가하는 부분 수열을 구할 수 있는다. 다음과 같을 것이다.

• 마지막 숫자가 3인 경우: { 3 } : 1
• 마지막 숫자가 5인 경우: { 3, 5 } : 2
• 마지막 숫자가 1인 경우: { 1 } : 1
• 마지막 숫자가 6인 경우: { 3, 5, 6 } : 3
• 마지막 숫자가 5인 경우: { 3, 5 } : 2
• 마지막 숫자가 7인 경우: { 3, 5, 6, 7} : 4
• 마지막 숫자가 4인 경우: { 1, 2, 4 } : 3

여기서 정답은 전체 길이 중 가장 큰 값인 4인 것을 알수 있지만 정답보다는 전체 과정을 먼저 정리해보자. 마지막 숫자가 5인 경우를 살펴보자. 마지막 숫자가 5인 경우는 5보다 작은 숫자(여기서는 3)로 끝나는 수열보다 1만큼 더 긴 수열을 가지고 있다. 마지막 숫자가 6인 경우도 마찬가지로 마지막 숫자가 6인 경우보다 작은 숫자(여기서는 5)로 끝나는 수열보다 1만큼 더 긴 수열을 가지고 있다.

 

마지막 숫자가 i인 경우의 값이 중복으로 사용됨을 확인할 수 있다. 이 값을 저장해두는 배열을 만들면 중복 계산을 줄일 수 있다. 즉 cache[i]는 마지막 숫자가 i번째 숫자로 끝나는 수열의 길이로 정할 수 있다. 그리고 cache[i]의 값은 cache 배열의 1 ~ i-1 마지막 숫자가 i번째 숫자보다 작은 값인 수들 중 최댓값 + 1이 될 수 있다.

예를 들어 마지막 숫자가 7인 경우를 살펴보자.

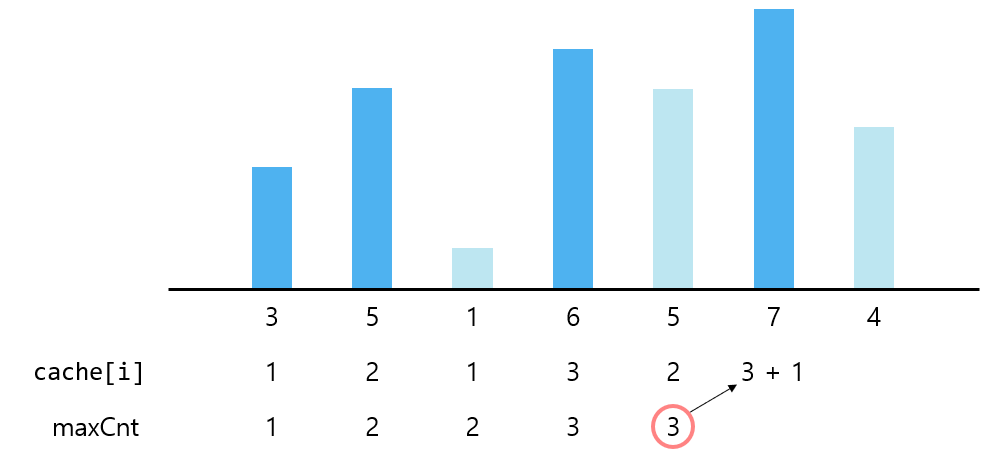
마지막 숫자가 7인 경우 보다 작은 값으로 끝나면서, 가장 큰 값을 가진 수는 마지막 숫자가 6으로 끝나는 경우임을 알 수 있다. 이를 코드로 구현하면 다음과 같다.

구현

#include <iostream>
#include <array>
#include <cmath>

#define endl '\n'
using namespace std;

int main() {
    // 입출력 성능 향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);

    array<int, 1'001> cache{};
    array<int, 1'001> a{};

    int N; //N (1 ≤ N ≤ 1,000)
    cin >> N;
    for (int i = 1; i <= N; ++i)
    {
        cin >> a[i];
    }
    int answer{};
    for (int i = 1; i <= N; ++i)
    {
        int maxCnt{};
        for (int j = 1; j < i; ++j)
        {
            if (a[i] > a[j])
            {
                maxCnt = max(cache[j], maxCnt);
            }
        }
        cache[i] = maxCnt + 1;
        answer = max(cache[i], answer);
    }

    cout << answer;

    return 0;
}

성능 개선

위의 알고리즘에서 maxCnt을 구하기 위해 a[i] > a[j] 이 비교문이 \(O(n^2)\)번 호출됨을 알 수 있다. 앞서 언급한바와 같이 이 알고리즘은 시간복잡도를 \(O(n\mbox{log}n)\)까지 개선할 수 있다. \(O(n\mbox{log}n)\)으로 개선된 알고리즘을 이해하기 위해서는 lower_bound함수를 사용해야 한다. lower_bound는 정렬되어 있는 배열에서 해당 원소가 삽입될 수 있는 위치들 중 가장 낮은 값의 반복자를 반환하는 함수이다.

예를 들어 {3, 4, 4, 5, 6}이라는 배열이 있고 lower_bound로 새로운 원소 4를 탐색하면 2번째 원소의 반복자가 반환된다. 그리고 이 lower_bound 함수는 이분 탐색(이분 탐색이기 때문에 반드시 정렬되어 있는 배열에서만 가능)을 하기 때문에 \(O(\mbox{log}n)\)의 탐색으로 위치를 찾을 수 있다. 이제 이 lower_bound 함수를 사용해서 성능을 개선해보자.

 

먼저 하나의 새로운 배열이 필요하다. 이 배열의 이름을 list라 하자. 이 배열에는 입력받은 수열들을 lower_bound함수를 사용해서 아래의 규칙대로 새로운 원소로 덮어 씌우거나 삭제할 것이다.

• list에 lower_bound로 탐색했을 때 비어있는 칸이라면
  • len을 1 증가시킨다.
• 탐색한 위치에 값을 넣는다.

수열 {3, 5, 1, 6, 5, 7, 4}에 대해서 예를 보이겠다.

수열 {3, 5, 1, 6, 5, 7, 4}

에서 첫 번째 원소 3을 lower_bound로 탐색하면 아직 list가 비었기 때문에 첫 번째 위치가 나올 것이다. 이를 그대로 삽입한다.

i: 1
list: { 3 } / len : 1

두 번째 원소 5를 lower_bound로 탐색하면 두번 째 원소 위치가 나올 것이다. 그리고 여기는 아직 비어있기 때문에 len을 1 증가시키고 삽입한다.

i: 2
list: { 3, 5 } / len : 2

세 번째 원소 1을 lower_bound로 탐색하면 첫 번째 위치가 나온다. 이때 첫 번째 위치는 이미 3이 차지하고 있다. 하지만 3을 1로 덮어 씌우자.

i: 3
list: { 1, 5 } / len : 2

네 번째 원소 6을 lower_bound로 탐색하면 세 번 째 위치가 나온다. 세번 째위치는 비었기 때문에 len을 1 증가시키고 세 번째 위치에 추가하자.

i: 4
list: { 1, 5, 6 } / len : 3

다섯 번째 원소 5를 lower_bound로 탐색하면 두 번째 위치가 나온다. 두번 째 위치는 이미 5가 있기 때문에 5를 5로 덮어 씌우자.

i: 5
list: { 1, 5, 6 } / len : 3

여섯 번째 원소 7을 lower_bound로 탐색하면 네 번째 위치가 나온다. 네번 째 위치는 비어있기 때문에 len을 1 증가시키고 네 번째 위치에 추가하자.

i: 6
list: { 1, 5, 6, 7 } / len : 4

마지막 원소 4를 lower_bound로 탐색하면 두 번째 위치가 나온다. 두 번 째 위치는 이미 5가 있기 때문에 5를 4로 덮어 씌우자

i: 7
list: { 1, 4, 6, 7 } / len : 4

아래의 그림처럼 list배열은 마치 기존의 수열을 압축한 모습을 보인다.

 

물론 list의 수열이 가장 긴 수열과 동일한 수열은 아니다. 하지만 가장 긴 수열과 길이는 항상 동일함이 보장된다. 그리고 전체 원소에 n에 대해서 lower_bound 함수를 호출하기 때문에 전체 시간 복잡도는 \(O(n\mbox{log}n)\)이 된다.

개선된 코드

#include <iostream>
#include <array>
#include <algorithm>

#define endl '\n'
using namespace std;

int main() {
    // 입출력 성능 향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);

    array<int, 1'001> arr{};
    array<int, 1'001> list{};

    int N; //N (1 ≤ N ≤ 1,000)
    cin >> N;

    for (int i = 1; i <= N; ++i)
    {
        cin >> arr[i];
    }

    int len{}; // list의 길이 
    for (int i = 1; i <= N; ++i)
    {
        auto lowerPos = lower_bound(list.begin(), list.begin() + len, arr[i]);

        if (*lowerPos == 0)
            len++;

        *lowerPos = arr[i];
    }

    cout << len;
    return 0;
}