[BOJ 2263] 트리의 순회(C++)

트리의 순회 (Gold 3)

문제

전체 문제 보기

2263번: 트리의 순회

접근법

이 문제는 트리의 중위 순회와 후위 순회 출력 값으로 트리의 전위 순회를 만드는 문제이다. 전위 순회는 루트 노드가 가장 먼저 출력되고, 중위 순회는 루트 노드가 중간에 출력되며, 후위 순회는 루트 노드가 가장 마지막에 출력된다는 특징을 가졌다. 아래의 그래프를 보자.

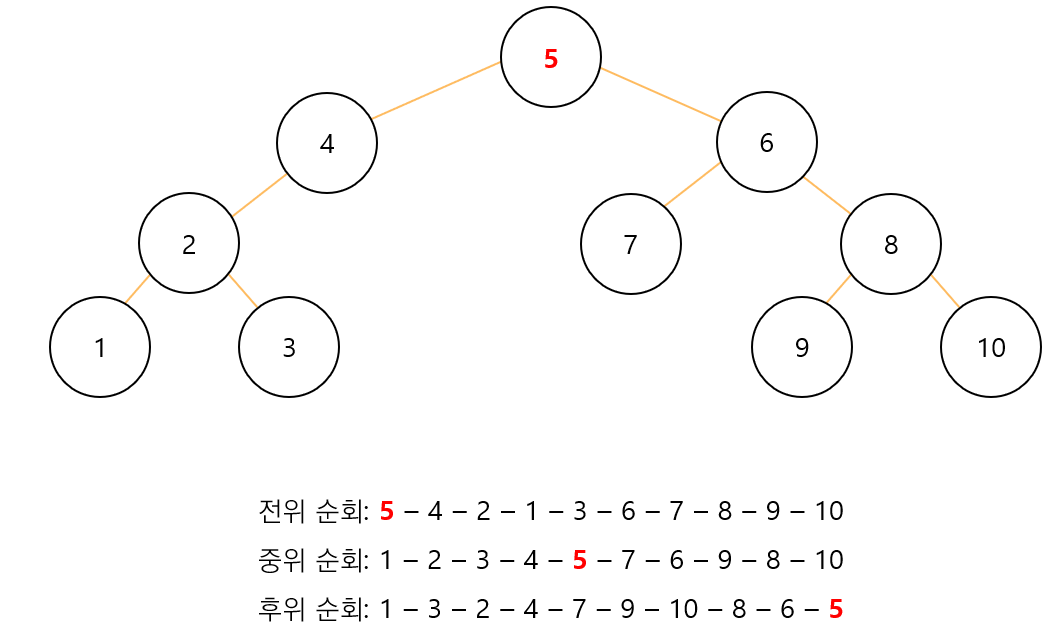
루트 노드 5가 후위 순회에서 가장 마지막에 출력됨을 알 수 있다. 우리는 이러한 특징을 활용하여 문제를 분할 정복으로 풀 수 있다.

• 후위 순회의 마지막 값을 루트 노드로 특정한다.
• 중위 순회에서 루트 노드를 탐색한다.
• 루트 노드의 왼쪽 값들을 루트 노드의 왼쪽 자식으로 호출하고, 오른쪽 값들을 루트 노드의 오른쪽 자식으로 호출한다.

그림으로 정리하면 다음과 같다.

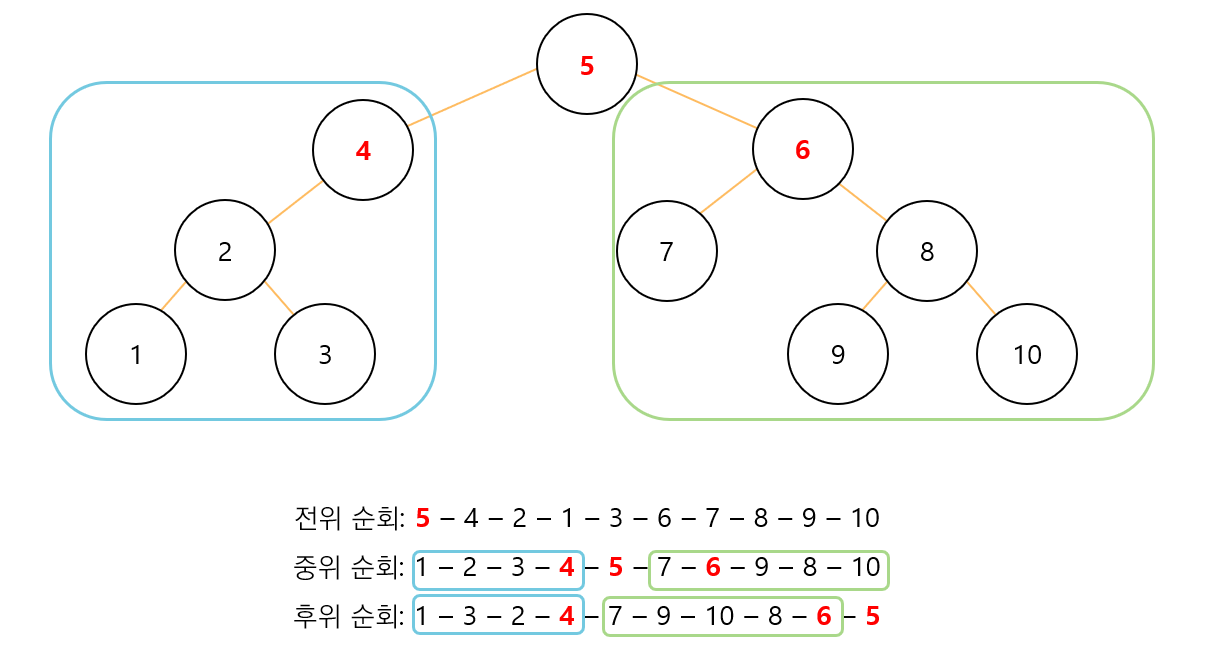
우리가 출력해야하는 값은 전위 순회 값이기 때문에 루트 노드의 값을 출력 후, 왼쪽 오른쪽 자식의 값을 출력하여 결과를 얻을 수 있다.

구현

코드로 정리하면 다음과 같다.

• 먼저 후위 순회의 마지막 노드를 root 노드로 특정한다.
• 루트 노드를 출력한다.
• 그리고 중위 순회에서 루트노드를 탐색한다.
• 중위 순회에서 탐색한 루트 노드의 왼쪽을 다시 PreOrder 함수로 탐색한다.
• 중위 순회에서 탐색한 루트 노드의 오른쪽을 다시 PreOrder 함수로 탐색한다.

vector<int> inOrder;
vector<int> postOrder;

void PreOrder(int inBegin, int postBegin, int size)
{
    if (size == 0)
        return;

    const int postEnd = postBegin + size - 1;
    int root = postOrder[postEnd];

    cout << root << " ";

    int leftSize{};
    while (root != inOrder[inBegin + leftSize])
    {
        leftSize++;
    }

    // 왼쪽 탐색
    PreOrder(inBegin, postBegin, leftSize);

    // 오른쪽 탐색
    const int rightInBegin = inBegin + leftSize + 1;
    const int rightPostBegin = postBegin + leftSize;
    const int rightSize = size - leftSize - 1;
    PreOrder(rightInBegin, rightPostBegin, rightSize);
}

개선

위 알고리즘에서 가장 많은 계산량을 사용하는 부분은 루트 노드를 탐색하는 while문이다. 이 알고리즘의 총 시간 복잡도는 \(O(n\mbox{log}n)\)이다. 이 알고리즘은 공간을 조금 더써 \(O(n)\) 시간 복잡도로 개선할 수 있다. 바로 inOrder배열의 인덱스를 값으로 가지고, inOrder의 값을 인덱스로 가지는 inOrderIdex 배열을 만드는 것이다. 모든 노드의 값이 1~n까지 중복없이 주어지기 때문에 아래와 같이 구현하는 것이 가능하다.

for (int i = 0; i < n; ++i)
{
    inOrderIdx[inOrder[i]] = i;
}

inOrderIdex 배열을 사용하면 leftSize를 반복문에서 탐색할 필요 없이 아래와 같이 인덱싱으로 값을 바로 구할 수 있다.

int leftSize = inOrderIdx[root] - inBegin;

\(O(n\mbox{log}n)\) 성능의 알고리즘을 \(O(n)\) 성능으로 향상한 결과 다음과 같이 시간을 줄일 수 있다.

구현

개선된 알고리즘으로 다음과 같이 구현할 수 있다.

#include <iostream>
#include <vector>

#define endl '\n'
using namespace std;
vector<int> inOrder;
vector<int> inOrderIdx;
vector<int> postOrder;

void PreOrder(int inBegin, int postBegin, int size)
{
    if (size == 0)
        return;

    const int postEnd = postBegin + size - 1;
    int root = postOrder[postEnd];

    cout << root << " ";

    int leftSize = inOrderIdx[root] - inBegin;


    // 왼쪽 탐색
    PreOrder(inBegin, postBegin, leftSize);

    // 오른쪽 탐색
    const int rightInBegin = inBegin + leftSize + 1;
    const int rightPostBegin = postBegin + leftSize;
    const int rightSize = size - leftSize - 1;
    PreOrder(rightInBegin, rightPostBegin, rightSize);
}


int main() {
    // 입출력 성능 향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);

    int n; // n(1 ≤ n ≤ 100,000)

    cin >> n;

    inOrder.resize(n);
    postOrder.resize(n);
    inOrderIdx.resize(n+1);

    for (int i = 0; i < n; ++i)
    {
        cin >> inOrder[i];
    }

    for (int i = 0; i < n; ++i)
    {
        cin >> postOrder[i];
    }

    for (int i = 0; i < n; ++i)
    {
        inOrderIdx[inOrder[i]] = i;
    }

    PreOrder(0, 0, n);

    return 0;
}