[BOJ 10844] (DP) 쉬운 계단 수 (C++)

쉬운 계단 수 (Silver 1)

문제

전체 문제 보기

10844번: 쉬운 계단 수

접근법

N자리의 계단수가 되기 위해서는 N자리에 숫자는 N-1자리의 숫자와 1만큼 차이가 나야 한다. 각 자릿수마다 끝자리 숫자를 기준으로 만들 수 있는 수의 개수를 카운트할 수 있다. 예를 들어 두 자릿수들 중 3으로 끝나는 계단 수는 23, 43 두 개가 존재하고, 5로 끝나는 계단 수는 45, 65가 존재한다. 그렇다면 세 자리 수중 4로 끝나는 계단수는 몇 개가 존재할까? 두 자리 수중 3으로 끝나는 수들의 개수와 5로 끝나는 수로 세 자릿수 중 4로 끝나는 계단 수를 만들 수 있기 때문에 총 4개를 만들 수 있다.(234, 434, 454, 654) 이를 그림으로 표현하면 아래와 같다.

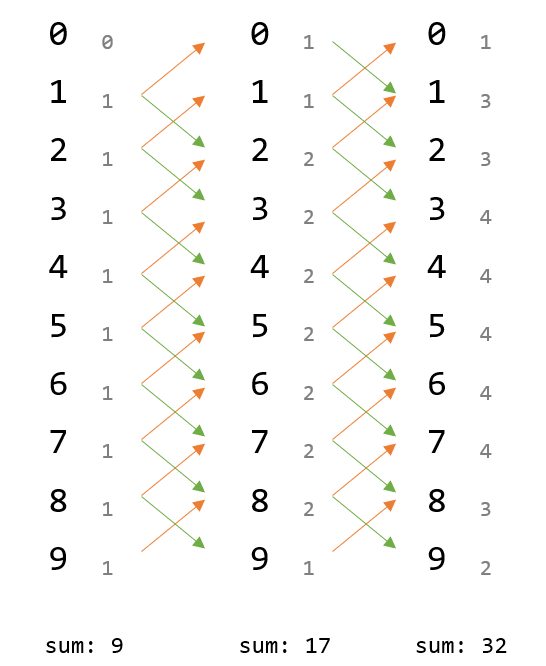
위 그림을 점화식으로 표현하면 다음 과 같다. (\(i\) - 자릿수, \(j\) - 끝자리 수(0~9))
\[f(i, j) = f(i - 1, j-1) + f(i - 1, j+1)\]

그리고 0과 9로 끝나는 수는 예외로 다뤄줘야한다. 끝자리가 0이 되기 위해서는 바로 앞자리 수로 1만 올 수 있고, 9가 되기 위해서는 앞 자릿수가 8만 올 수 있기 때문이다. 이를 구현하면 다음과 같다.

구현

정답에서 결과값에 1,000,000,000을 나눈 나머지를 요구하고 있다. 각 값들이 지수적으로 증가하기 때문에 모든 계산 결과에 1,000,000,000의 나머지를 구하여 오버플로를 방지하자.(나머지 연산은 결합 법칙이 성립하기 때문에 계산 중간중간에 나머지를 구하더라도 전체 계산 결과는 동일하다.)

#include <iostream>
#include <array>
#define endl '\n'

using namespace std;
int main()
{
    //입출력 성능향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);
    const int MAX = 101;
    const int MOD = 1'000'000'000;

    array<array<int, 10>, MAX> cache{};
    int N; //N은 1보다 크거나 같고, 100보다 작거나 같은 자연수
    cin >> N;

    cache[1].fill(1);
    cache[1][0] = 0;

    for (int i = 2; i <= N; ++i)
    {
        cache[i][0] = cache[i - 1][1] % MOD;
        for (int j = 1; j < 9; j++)
        {
            cache[i][j] = (cache[i - 1][j-1] + cache[i - 1][j+1]) % MOD;
        }
        cache[i][9] = cache[i - 1][8] % MOD;
    }

    int sum = 0;
    for (int i = 0; i <= 9; ++i)
    {
        sum += cache[N][i];
        sum %= MOD;
    }
    cout << sum;
    return 0;
}

성능 평가

모든 자리수(N)에 대해서 각 수들 (0~9)에 덧셈 연산을 진행한다. 따라서 전체 시간 복잡도는 \(O(n)\)이며 이를 저장하기 위한 배열을 가지고 있기 때문에 공간 복잡도 또한 \(O(n)\)이다.