이분 그래프(Gold 4)
문제
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K(2≤K≤5)가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V(1≤V≤20,000)와 간선의 개수
www.acmicpc.net
접근법
문제를 읽고 이분 그래프가 무엇인지 감이 오지 않는다면 이 글을 참고하자. 위키백과: 이분 그래프. 이 글에 따르면 이분 그래프는 다음과 같은 특징을 가진다.
모든 노드는 빨간색 혹은 파랑색을 가지며, 한 노드의 인접한 노드는 서로 다른 색상을 가져야 한다.
우리는 이 특징을 활용하여 다음과 같이 BFS로 문제를 풀 수 있다.
- 한 번도 방문하지 않은 노드는 색상을 가지지 않는다.
- 처음 노드를 파랑색으로 칠한 후 큐에 넣는다.
- 큐가 빌때까지 반복한다.
- 큐에서 꺼낸 노드가 인접 노드의 색상과 같다면 이분 그래프가 아니므로
false를 반환한다. - 큐에서 꺼낸 노드의 인접 노드에 색상이 없다면, 큐에서 꺼낸 노드와 다른 색상을 칠하고 큐에 넣는다.
- 반복문이 종료될때까지
false가 반환되지 않았다면 이분 그래프 이므로true를 반환한다.
그리고 여기서 한 가지 더 고려해야 할 사항이 있다. 모든 노드가 연결되지 않은 경우가 존재할 수 있다. 아래와 같은 예시도 입력으로 주어질 수 있다.
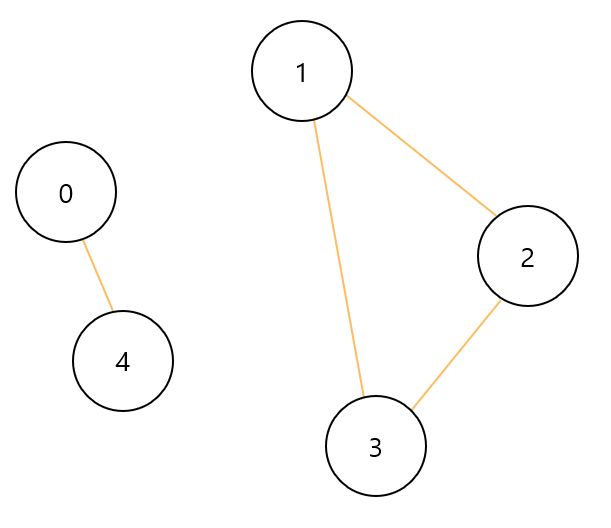
아래의 경우 1, 2, 3 노드 때문에 이분 그래프가 안된다. 하지만 0번 노드에서 BFS탐색을 시작한다면 1, 2, 3번 노드에 대해서는 탐색을 진행하지 못하고 true를 반환하게 된다. 때문에 1번 부터 모든 노드가 한 가지의 색상을 가질 수 있도록 탐색을 진행해야 한다.
자료구조 선택
먼저 BFS에서 사용할 노드 구조체를 결정하기 위해 다음 사항을 고려했다.
- 모든 노드는 빨간색 혹은 파란색 색상을 가진다.
- 그리고 인접 노드가 몇 개 연결될지 알 수 없다.
enum class Color : uint8_t
{
None,
Red,
Blue,
MAX
};
struct Node {
Node() : color(Color::None)
{}
Color color;
// 인접노드의 인덱스
vector<int> adjacent;
};그리고 Graph 클래스에서는 모든 노드를 배열로 관리한다. 각 노드들은 이 배열의 인덱스를 가지고 인접 노드에 접근할 수 있다.
InputData멤버 함수: 데이터를 입력받아 노드들을 연결한다.IsBipartite멤버 함수: 모든 노드에 색상을 칠하면서 이분 그래프라면true, 아니면false를 반환한다.BFS멤버 함수:IsBipartite함수에서 호출되며start노드에서 시작하여start노드와 연결된 노드들은 모두 하나의 색을 칠한다. 과정에서 이분 그래프가 아님이 확인되면false를 반환한다.
class Graph {
public:
Graph() {}
void InputData(); // 데이터 입력 받아서 간선 연결
bool IsBipartite(); // 이분 그래프인지 판단
private:
bool BFS(int start); // start에서 시작한 노드가 이분그래프라면 true 반환
static const int MAX_VERTEX = 20'001;
int V, E; // 1 <= V <= 20'000 / 1 <= E <= 200'000
array<Node, MAX_VERTEX> nodes{};
};이 클래스는 메인 함수에서 다음과 같이 사용된다.
int main() {
int K; // 테스트 케이스
cin >> K;
while (K--)
{
Graph graph;
graph.InputData();
if (graph.IsBipartite())
cout << "YES" << endl;
else
cout << "NO" << endl;
}
return 0;
}전체 소스 코드
아래와 같이 구현할 수 있다.
#include <iostream>
#include <vector>
#include <array>
#include <queue>
#define endl '\n'
using namespace std;
enum class Color : uint8_t
{
None,
Red,
Blue,
MAX
};
struct Node {
Node() : color(Color::None)
{}
Color color;
// 인접노드의 인덱스
vector<int> adjacent;
};
class Graph {
public:
Graph() {}
void InputData();
bool IsBipartite();
private:
bool BFS(int start); // start에서 시작한 노드가 이분그래프라면 true 반환
static const int MAX_VERTEX = 20'001;
int V, E; // 1 <= V <= 20'000 / 1 <= E <= 200'000
array<Node, MAX_VERTEX> nodes{};
};
void Graph::InputData()
{
cin >> V >> E;
// E 개수만큼 간선 연결
int a, b;
for (int i = 0; i < E; ++i)
{
cin >> a >> b;
nodes[a].adjacent.push_back(b);
nodes[b].adjacent.push_back(a);
}
}
bool Graph::IsBipartite()
{
for (int i = 1; i <= V; ++i)
{
if (nodes[i].color == Color::None)
{
if (BFS(i) == false)
return false;
}
}
return true;
}
bool Graph::BFS(int start)
{
queue<int> q;
nodes[start].color = Color::Blue;
q.push(start);
while (!q.empty())
{
int cur = q.front();
q.pop();
for (int next : nodes[cur].adjacent)
{
if (nodes[cur].color == nodes[next].color)
{
return false;
}
if (nodes[next].color == Color::None)
{
if (nodes[cur].color == Color::Blue)
nodes[next].color = Color::Red;
else
nodes[next].color = Color::Blue;
q.push(next);
}
}
}
return true;
}
int main() {
// 입출력 성능 향상을 위한 설정
ios_base::sync_with_stdio(false);
cout.tie(NULL);
cin.tie(NULL);
int K; // 테스트 케이스
cin >> K;
while (K--)
{
Graph graph;
graph.InputData();
if (graph.IsBipartite())
cout << "YES" << endl;
else
cout << "NO" << endl;
}
return 0;
}성능 평가
이 풀이의 시간 복잡도를 살펴보자. 이 알고리즘에서 가장 많은 비용을 차지하는 부분은 BFS에서 사용된 반복문이다. 첫 번째 반복문인 while문은 모든 노드(\(N\))에 대해서 한번씩 수행된다. 그리고 while문 안의 for문은 모든 간선(\(E\))에 대해서 한번 씩 수행된다. 때문에 시간 복잡도는 \(O(N + E)\)로 나타낼 수 있다. 공간 복잡도 또한 간선의 수의 두배 만큼과, 모든 노드의 개수 만큼의 공간이 필요하기 때문에 \(O(N + E)\)로 나타낼 수 있다.
