[BOJ 1904] 01타일(C++)

01타일 (Silver 3)

문제

전체 문제 보기

1904번: 01타일

접근법

이번 문제에서 구해야 하는 값은 1 타일과 00 타일을 활용해서 자릿수 N이 주어졌을 때 지원이가 만들 수 있는 모든 이진수 가짓수이다. 여기서 N의 값은 1,000,000 이하의 자연수로 꽤 크다. 그래서 자릿수 N이 주어졌을 때 지원이가 만들 수 있는 이진수의 최댓값은 \(2^1,000,000\)으로 모든 경우의 수를 따져보는 것은 불가능하다. 때문에 우리는 임의의 N에서 만들 수 있는 이진수의 가짓수 규칙을 살펴봐야겠다. N이 1,2,3,4인 경우 만들 수 있는 이진수는 아래와 같다.

▲ N 이 1,2,3,4인 경우 만들 수 있는 이진수

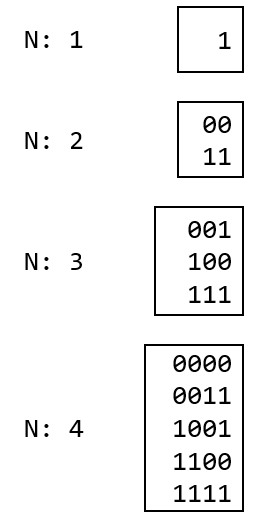
여기서 우리는 한 가지 규칙을 찾을 수 있다.
아래의 N이 3인 경우를 살펴보자.

▲ N이 3인 경우 만들 수 있는 이진수

N이 3인 경우는 N이 1일때 만들 수 있는 수 앞에 00 카드를 붙인 수와 N이 2일때 만들 수 있는 수 앞에 1카드를 붙인 수로 구성되어 있다. N이 4인 경우에도 마찬가지 규칙이 적용되고 있음을 확인할 수 있다.

 

N이 4인 경우도 N이 2일때 만들 수 있는 수 앞에 00카드를 붙인 수와 N이 3일때 만들 수 있는 수 앞에 1카드를 붙인 수로 구성되어 있다.

▲ N이 4인 경우 만들 수 있는 이진수

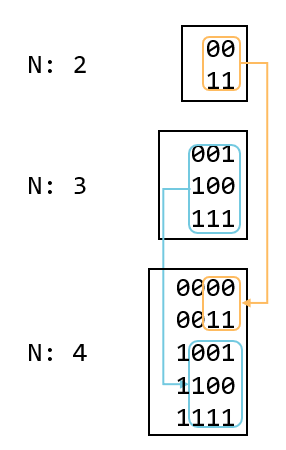
이제 일반화를 시켜보자. 우리가 구해야 하는 것은 오로지 만들 수 있는 이진수의 가짓수이다. 따라서 \(f(n)\)은 임의의\(n\)에 대해서 만들 수 있는 이진수의 경우의 수라고 했을 때 아래와 같이 피보나치수열과 같은 점화식을 유도할 수 있다. (초기값은 피보나치와 다르다.)

 

\[f(n)= \begin{cases} 1, & \mbox{if } n = 1 \\ 2, & \mbox{else if } n = 2 \\f(n-1) + f(n-2), & \mbox{else } \end{cases}\]

구현

점화식을 Bottom-up 방식으로 다음과 같이 구현할 수 있다. %연산은 결합 법칙이 성립하기 때문에 연산을 진행할 때마다 %한 값과 최종 합에 %한 값은 동일하다. 오버플로우를 방지하고, 불필요한 if 비교 연산을 피하기 위해서 모든 cache 값에 %연산을 하였다.

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    vector<int> cache;
    cache.resize(1'000'001);

    int N; // 지원이가 만들 수 있는 길이 (1 <= N <= 1'000'000)

    cache[1] = 1;
    cache[2] = 2;

    cin >> N;

    for (int i = 3; i <= N; ++i)
    {
        cache[i] = cache[i - 2] + cache[i - 1];
        cache[i] = cache[i] % 15746;
    }

    cout << cache[N];

    return 0;
}

성능 개선

위 코드의 시간 복잡도는 \(O(n)\)임을 쉽게 확인할 수 있다. 그리고 공간 복잡도 또한 int변수가 N개만큼 필요하기 때문에 \(O(n)\)이다. 하지만 이번 문제에서는 공간 복잡도를 \(O(1)\)까지 최적화할 수 있다.

 

우리가 동적 계획법 문제에서 캐싱을 하는 이유는 중복 연산을 피하기 위해서 한 번 계산한 결과를 저장해두기 위함이다. 그런데 잘 살펴보면 중복해서 연산이 호출되는 경우가 딱 한번뿐이다. 그것도 n 번째에 n-1과 n-2가 호출되었다면 n-1은 바로 다음 n+1 번째 계산 때 한번 더 호출될 뿐이다. 그렇기 때문에 굳이 int타입을 1,000,001개 사용하는 배열을 사용할 필요 없이 다음과 같이 int변수 3개만으로 N번째 값을 구할 수 있다. 아래는 성능을 개선한 코드이다.

#include <iostream>
using namespace std;

int main()
{
    int N; // 지원이가 만들 수 있는 길이 (1 <= N <= 1'000'000)
    cin >> N;

    int a = 1, b = 1, c = 1;

    for (int i = 2; i <= N; ++i)
    {
        c = a + b;
        c = c % 15746;

        a = b;
        b = c;
    }

    cout << c;

    return 0;
}