법선 벡터의 변환
3D 물체의 버텍스 정보에는 위치정보와 함께 법선 벡터 정보가 들어갈 수 있다. 버텍스에 변환(이동, 회전, 스케일)을 적용할 때 위치정보는 변환을 그대로 적용하면 원하는 좌표로 이동이 가능하다. 하지만 버텍스 정보에 변환을 적용할 때 "비균등 스케일" 인 경우 변환 행렬의 "역전치 행렬"을 적용해야 한다. 이번 글에서는 이러한 이유를 다룬다.
법선 벡터의 비균등 스케일 적용 시 문제점
법선벡터에 비균등 스케일 변환 행렬\(A\)(\(x,y,z\) 의 크기가 다른 경우)를 적용하면 다음과 같이 표면에 대한 수직이 유지되지 않는다.
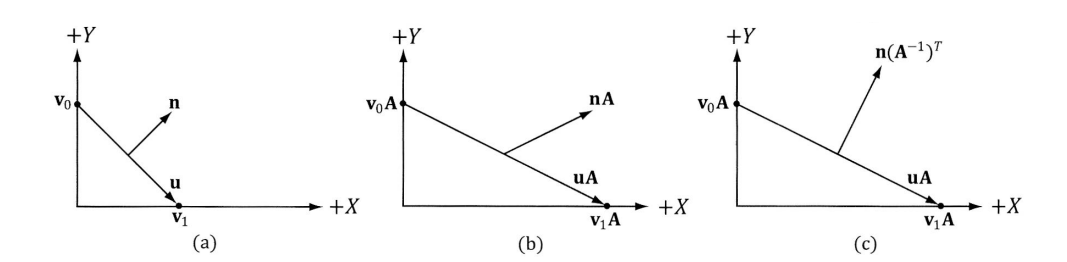
역전치 행렬을 사용 이유
법선 벡터에는 변환 행렬\(A\)를 역전치를 적용 후 \((A^{-1})^T\) 곱하면 표면과 직각을 유지할 수 있다.
역전치 행렬을 사용할 경우 직각이 유지되는 이유를 아래의 유도과정으로 살펴본다.
유도 과정
법선 벡터를 적용할 새로운 변환행렬을 \(X\) 할 때 그 유도식은 다음과 같다.
| \(uA \cdot nX = 0\) | ||
| \(u \cdot v = 0 \) | 표면 벡터와 법선 벡터가 직교 | |
| \(un^T = 0 \) | 벡터 내적을 행렬 곱셈 형태로 표현 | |
| \(u(AA^{-1})n^T = 0 \) | 단위 행렬 \(I = AA^{-1}\) | |
| \((uA)(A^{-1}n^{T}) = 0\) | 행렬곱셈의 배분 법칙 | |
| \((uA)((A^{-1}n^{T})^{T})^{T} = 0\) | 전치 항등식 \((A^T)^T = A\) 적용 | |
| \((uA)(n(A^{-1})^T)^T = 0\) | 전치 항등식 \((AB^T)^T = BA^T\) 적용 | |
| \(uA \cdot n(A^{-1})^T = 0\) | 행렬 곱셈을 벡터 내적 형태로 표현 | |
| \( \therefore X = (A^{-1})^T\) | ||
위와 같은 이유로 법선 벡터에 변환 행렬을 적용할 때는 변환 행렬의 역전치 행렬을 적용해야 한다.
출처:
한빛미디어 출판: <DirectX 12를 이용한 3D 게임 프로그래밍 입문>
