[BOJ 1525] 퍼즐 (C++)

퍼즐(Gold 2)

문제

전체 문제 보기

1525번: 퍼즐

접근법

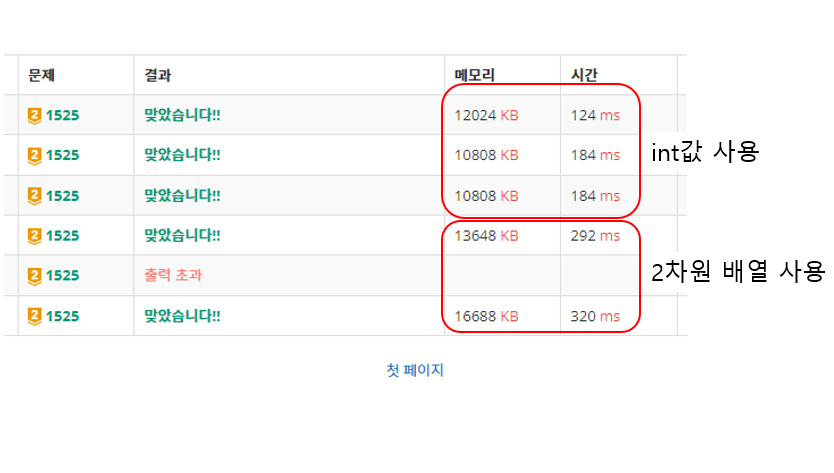
퍼즐이 한 칸씩 움직이는 경우에 대해서 너비 우선 탐색을 진행하여 최소 거리를 구할 수 있는 문제입니다. 퍼즐의 모양을 저장하기 위해서 2차원 배열을 사용할 수 있지만 1~9까지 수를 9개 저장하고 비교하기 위해서 배열을 사용하는 것은 공간과 시간에 낭비가 발생합니다. 반면 000,000,000 ~ 999,999,999까지 사용할 수 있는 4바이트 int 타입 하나로 퍼즐을 나타내고 값을 비교한다면 9개의 정수 배열을 활용하는 것에 비해 사용하는 공간과 시간을 많이 절약할 수 있습니다.

3*3 퍼즐을 다음과 같이 표현할 수 있습니다.

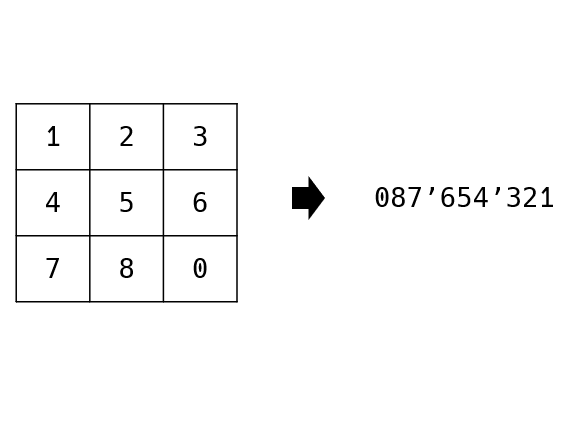
3*3 퍼즐을 int 값으로 변환하는 방법은 다음과 같습니다.

int MapToInt(const Map& map)
{
    int fac = 1;
    int retval{};
    for (int i = 0; i < 3; ++i)
    {
        for (int j = 0; j < 3; ++j)
        {
            retval += map[i][j] * fac;
            fac *= 10;
        }
    }
    return retval;
}

이제 이 int 값으로 BFS 탐색을 실행할 수 있습니다. BFS 탐색 코드는 아래에서 확인할 수 있습니다.

전체 코드

#include <iostream>
#include <queue>
#include <array>
#include <unordered_set>
#include <algorithm>
#include <cmath>
#define endl "\n"
using namespace std;

struct Pos {
    Pos() {}
    Pos(int _r, int _c) : r{ _r }, c{ _c }{}
    int r{};
    int c{};
    Pos& operator+= (const Pos& other)
    {
        r += other.r;
        c += other.c;
        return *this;
    }
};
Pos operator+(const Pos& lhs, const Pos& rhs)
{
    return Pos(lhs.r + rhs.r, lhs.c + rhs.c); 
}
using Map = array<array<int, 3>, 3>;
struct Move {
    int dep{};
    Pos zero{};
    int i_map;
};

Map puz;
unordered_set<int> vis;
const array<Pos, 4> dir{ Pos(1,0),Pos(-1,0),Pos(0,1),Pos(0,-1) };

int MapToInt(const Map& map)
{
    int fac = 1;
    int retval{};
    for (int i = 0; i < 3; ++i)
    {
        for (int j = 0; j < 3; ++j)
        {
            retval += map[i][j] * fac;
            fac *= 10;
        }
    }
    return retval;
}
bool IsOut(const Pos& pos)
{
    if (0 <= pos.c && pos.c < 3 && 0 <= pos.r && pos.r < 3)
        return false;
    else
        return true;

}
void Shift(int& i_map, Pos& cur, const Pos& dir)
{
    Pos next = cur + dir;
    int curIdx = cur.c + cur.r * 3;
    int nextIdx = next.c + next.r * 3;

    int nextFac = pow(10, nextIdx);
    int nextVal = i_map / nextFac;
    nextVal -= ((int)(nextVal / 10)) * 10;

    int curFac = pow(10, curIdx);

    // 0위치에 nextval 삽입
    i_map += nextVal * curFac;
    // nextval 위치를 0으로 설정
    i_map -= nextVal * nextFac;

    // zero 위치 이동
    cur += dir;
}
void printMap(int i_map)
{
    for (int i = 0; i < 3; ++i)
    {
        for (int j = 0; j < 3; ++j)
        {
            cout << i_map % 10 << " ";
            i_map /= 10;
        }
        cout << endl;
    }
    cout << endl;
}

int BFS()
{
    Map target_Map;
    target_Map[0] = { 1,2,3 };
    target_Map[1] = { 4,5,6 };
    target_Map[2] = { 7,8,0 };
    int i_target = MapToInt(target_Map);

    Move start;
    start.i_map = MapToInt(puz);
    for (int i = 0; i < 3; ++i)
        for (int j = 0; j < 3; ++j)
            if (puz[i][j] == 0)
            {
                start.zero.r = i;
                start.zero.c = j;
                break;
            }
        
    start.dep = 0;

    if (start.i_map == i_target) return 0;

    queue<Move> q;
    vis.insert(start.i_map);
    q.push(start);
    while(!q.empty())
    {
        Move cur = q.front();
        q.pop();
        //printMap(cur.i_map);
        for (int i = 0; i < 4; ++i)
        {
            if (IsOut(cur.zero + dir[i])) continue;
            Move next = cur;

            Shift(next.i_map, next.zero, dir[i]);

            next.dep += 1;
            if (vis.find(next.i_map) != vis.end()) continue;
            vis.insert(next.i_map);
            if (next.i_map == i_target) return next.dep;
            q.push(next);
        }
    }
    return -1;
}
int main() 
{
    //입출력 성능향상을 위한 설정
    ios_base::sync_with_stdio(false);
    cout.tie(NULL);
    cin.tie(NULL);
    for (auto& row : puz)
    {
        for (int& n : row)
        {
            cin >> n;
        }
    }

    int answer = BFS();
    cout << answer << endl;
    return 0;
}