토마토 (Silver 1)
문제
7569번: 토마토
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N과 쌓아올려지는 상자의 수를 나타내는 H가 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M ≤ 100, 2 ≤ N ≤ 100,
www.acmicpc.net
접근법
이 문제는 BFS 탐색을 통해서 상자에 들어있는 모든 토마토가 익을 때까지 걸리는 시간을 계산해야 하는 문제이다. 일반적인 BFS와 가장 큰 차이점은 탐색을 시작하는 지점이 1개 이상이 될 수 있다는 점이다. 기본적인 DFS/BFS 구현에 대한 이해가 필요하다면 이 글을 참고하자. 아래의 그림은 일반적인 BFS의 탐색이다.
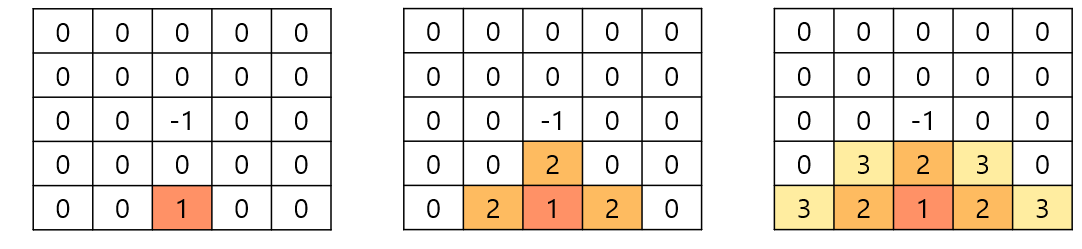
하지만 이 문제에서는 익은 토마토가 여러 개 일 수 있기 때문에 탐색을 시작하는 지점이 아래와 같이 2개 이상이 될 수도 있다.
때문에 일반적인 BFS에서는 큐에 시작 노드 하나만 넣고 시작했다면, 이 문제에서는 익은 토마토 노드를 모두 큐에 삽입하고 시작해야 한다.
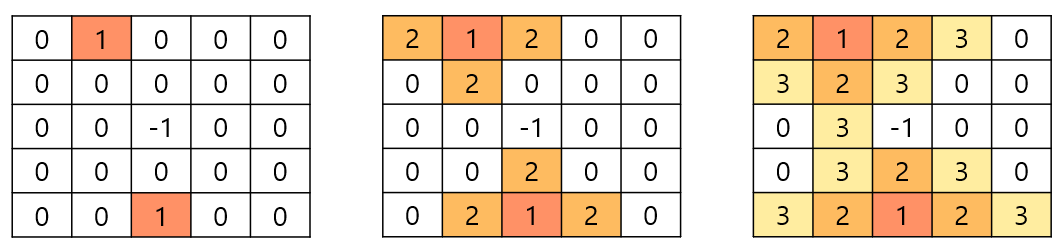
그리고 이 BFS에서 탐색을 진행하면 BFS 탐색의 깊이는 경과된 날짜와 동일하다.(하루에 바로 인접한 토마토에만 영향을 주기 때문) 때문에 각각의 토마토 Node는 방문 여부 기록, 토마토의 존재 여부, 탐색의 깊이를 기록할 수 있는 int 타입의 변수를 가지면 유용하게 활용할 수 있다.
구현
기본 자료구조로 활용할 토마토(Node)와 Node가 담길 NodeMap의 타입을 3차원 벡터 타입으로 아래와 같이 선언한다.
(2021.08.19 추가: 아래의 코드는 더 최적화 할 수 있으며 관련 내용을 보시려면 여기를 참조해 주세요. → [BOJ7576] (DFS/BFS) 토마토 (C++) 최적화)
struct Node {
Node(int mNum)
: mNum(mNum) // 노드를 생성할 시 노드에 할당할 번호를 입력받음.
{
mAdjacent.reserve(6); // 인접노드는 최대 6개까지 입력가능하기 때문에 6개 인접노드 미리 할당
}
vector<Node*> mAdjacent; // 인접 노드에 대한 정보
int mNum; // 토마토 깊이 정보 (1 이상: 익은 토마토, 0: 익지 않은 토마토, -1: 토마토 없음)
};
// 3차원 박스를 표현하기 위한 맵
using NodeMap = vector<vector<vector<Node*>>>;그리고 인접 노드의 설정은 최대 상, 하, 좌, 우, 앞, 뒤로 6개까지 가능하다. 반복문을 통해서 노드를 생성한 다음 아래와 같이 인접 노드를 설정해주자.
// 인접노드 설정
for (int h = 0; h < H; ++h)
{
for (int n = 0; n < N; ++n)
{
for (int m = 0; m < M; ++m)
{
if (h > 0)
{
map[h][n][m]->mAdjacent.push_back(map[h - 1][n][m]);
}
if (h < H - 1)
{
map[h][n][m]->mAdjacent.push_back(map[h + 1][n][m]);
}
if (n > 0)
{
map[h][n][m]->mAdjacent.push_back(map[h][n - 1][m]);
}
if (n < N - 1)
{
map[h][n][m]->mAdjacent.push_back(map[h][n + 1][m]);
}
if (m > 0)
{
map[h][n][m]->mAdjacent.push_back(map[h][n][m - 1]);
}
if (m < M - 1)
{
map[h][n][m]->mAdjacent.push_back(map[h][n][m + 1]);
}
}
}
}그리고 다음으로 주목할 부분은 BFS함수 구현 부분이다. 일반적인 BFS와 달리 아래와 같이 초기에 익은 토마토들을 모두 push()해주자.
int BFS(NodeMap& map)
{
int answer = 0;
queue<Node*> q;
// 익은 토마토는 모두 큐의 초기 탐색 노드로 push
for (auto box : map)
{
for (auto row : box)
{
for (auto node : row)
{
if (node->mNum == 1)
{
q.push(node);
}
}
}
}
// 큐가 빌때까지 탐색 시작
while (!q.empty())
//... (생략) ...이상으로 주목해서 살펴볼 지점에 대한 설명을 마치고 추가적인 설명은 아래의 전체 코드에 있는 주석을 참고하자.
#include <iostream>
#include <vector>
#include <queue>
#define endl '\n'
using namespace std;
struct Node {
Node(int mNum)
: mNum(mNum) // 모든 노드는 노드에 할당된 번호를 0으로 초기화.
{
mAdjacent.reserve(6); // 인접노드는 최대 6개까지 입력가능하기 때문에 6개 인접노드 미리 할당
}
vector<Node*> mAdjacent; // 인접 노드에 대한 정보
int mNum; // 토마토 깊이 정보 (1 이상: 익은 토마토, 0: 익지 않은 토마토, -1: 토마토 없음)
};
// 3차원 박스를 표현하기 위한 맵
using NodeMap = vector<vector<vector<Node*>>>;
int BFS(NodeMap& map)
{
int answer = 0;
queue<Node*> q;
// 익은 토마토는 모두 큐의 초기 탐색 노드로 push
for (auto box : map)
{
for (auto row : box)
{
for (auto node : row)
{
if (node->mNum == 1)
{
q.push(node);
}
}
}
}
// 큐가 빌때까지 탐색 시작
while (!q.empty())
{
Node* cur;
cur = q.front();
q.pop();
for (auto neighbor : cur->mAdjacent)
{
if (neighbor->mNum == 0)
{
neighbor->mNum = cur->mNum + 1;
q.push(neighbor);
answer = neighbor->mNum - 1;
}
}
}
return answer;
}
int main() {
// 입출력 성능 향상을 위한 설정
ios_base::sync_with_stdio(false);
cout.tie(NULL);
cin.tie(NULL);
// M: 가로 (2 ~ 100)
// N: 세로 (2 ~ 100)
// H: 높이 (1 ~ 100)
int M, N, H;
NodeMap map;
cin >> M >> N >> H;
// 노드 동적 할당
map.resize(H);
for (int h = 0; h < H; ++h)
{
map[h].resize(N);
for (int n = 0; n < N; ++n)
{
map[h][n].resize(M);
for (int m = 0; m < M; ++m)
{
int num;
cin >> num;
map[h][n][m] = new Node(num);
}
}
}
// 인접노드 설정
for (int h = 0; h < H; ++h)
{
for (int n = 0; n < N; ++n)
{
for (int m = 0; m < M; ++m)
{
if (h > 0)
{
map[h][n][m]->mAdjacent.push_back(map[h - 1][n][m]);
}
if (h < H - 1)
{
map[h][n][m]->mAdjacent.push_back(map[h + 1][n][m]);
}
if (n > 0)
{
map[h][n][m]->mAdjacent.push_back(map[h][n - 1][m]);
}
if (n < N - 1)
{
map[h][n][m]->mAdjacent.push_back(map[h][n + 1][m]);
}
if (m > 0)
{
map[h][n][m]->mAdjacent.push_back(map[h][n][m - 1]);
}
if (m < M - 1)
{
map[h][n][m]->mAdjacent.push_back(map[h][n][m + 1]);
}
}
}
}
int answer;
answer = BFS(map);
for (auto box : map)
{
for (auto row : box)
{
for (auto node : row)
{
// 탐색 종료후에도 남은 토마토가 있다면 -1 반환
if (node->mNum == 0)
answer = -1;
// 동적할당한 노드 삭제
delete node;
}
}
}
cout << answer;
return 0;
}
